Weird (or not) issues in thin-walled cylindrical shell buckling modes

[Vigardo]

TL;DR

Would you explain why I observe weird issues in the buckling modes of a thin-walled cylindrical shell? Are they physically sound?

Dear FEA experts,

I’m trying to analyse* some finite elements model of a thin walled cylinder with variable cross-section, but I’m observing four weird issues in the buckling modes. The structure is vertically (along z-axis) and horizontally (along y-axis) loaded on top. Would you help me to understand why? Thanks!

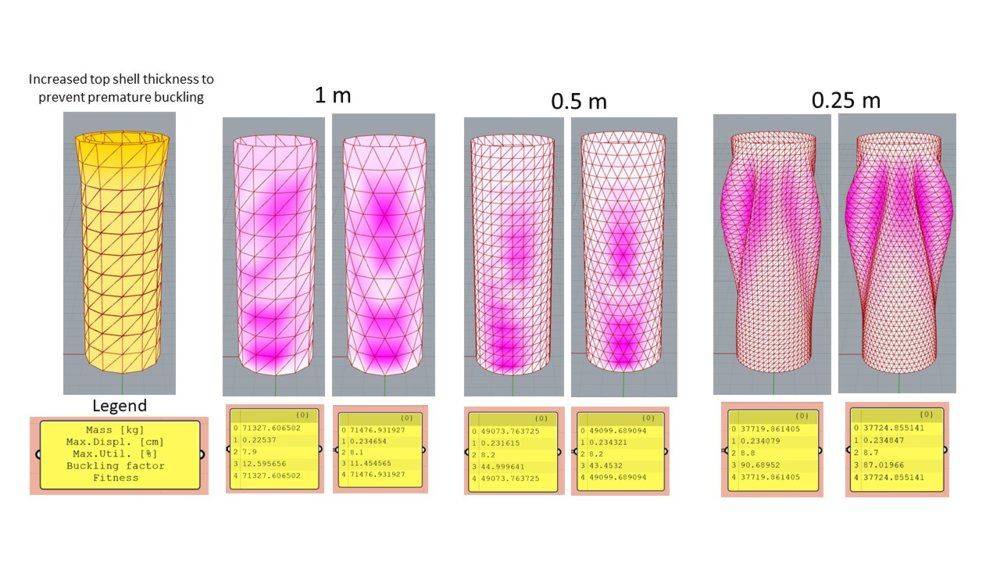
1. The lowest buckling factor (BF) increases as the mesh size decreases from 1 to 0.25 m (row number "3" in the yellow panels). Shouldn't it happen exactly the opposite? Shouldn't the structure be less stiff as element size is reduced?
2. In addition, it happens an abrupt change in the lowest buckling mode shape for mesh sizes finer that 0.35 m. This is accompanied by an steady increase in BF until about 0.25 or 0.1 m element size, where it converges to around 85-90 values. Note that the observed increase in BF (issue 1.) also occurs without mode shape change.
3. I tried two different triangular meshing patterns: Mesh-UV (left) and Alternate (right). It is apparent that the ripples of the first buckling mode are a bit twisted from the y-axis (green line, the direction of the horizontal load) for Mesh-UV meshing pattern. Only the Alternate meshing produces the expected horizontal ripples (because of loads symmetry). Would this be caused by the different triangular meshing?
4. As expected, the maximum displacements and utilisation (row "1" and "2" in yellow panels) are the same in all of them. However, the BFs are slightly different (around 5%) between Alternate and UV meshes, even at the finer mesh size. Shouldn't they converge?

*Using Karamba3D parametric engineering plugin (FEA) for Grasshopper/Rhino. Top ring elements are much thicker (50 cm) to prevent premature local buckling.

 

[Baluncore]

If the mesh is too coarse when compared with the radius of curvature you will be seeing the effect of the mesh size rather than the modeled object in the real world.

The fact that the numerical model changes behaviour is an indication that the model is failing at some mesh size. It is important to test the model sensitivity to mesh size. That is exactly what you have done and observed.

We know that too coarse a mesh will fail, and that too fine a mesh will work, but then computation will take too long. Trying to explain why a coarse mesh fails, in the particular way it does, is probably not a sensible use of your time.

 

[Vigardo]

You're right, perhaps I'm overthinking here. I will use the finer mesh for my calculations and not worry about the coarser mesh artefacts anymore. In fact, the finer mesh buckling factors are not so different (90 and 87) for both mesh types. Thank you very much for your kind explanation!