Weird thinking of electric field inside a hollow cylinder.

[TwoEG]

While I was studying with electric field about cylinder, I learned that for a very long cylinder, the electric field in the hollow of cylinder will be zero.

http://physics.stackexchange.com/questions/156789/electric-field-of-hollow-cylinder

However, I couldn't accept this intuitively, and thought up this weird idea.

We can express electric field E of charged line like

$E=\frac \lambda {2\pi\epsilon_0 r}$

Thus, we knows that (+) charge between two parallel lines with same charge density will always move to their center, right?

Then, suppose we have a (+) charge in a cylinder other than on its axis, and let's see that cylinder above from it.

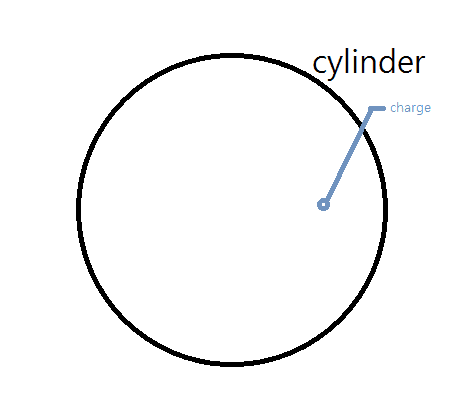
And this is what really confuses me.

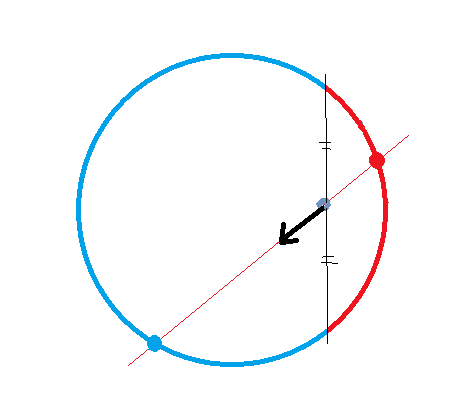
Draw a line that passes charge, then it'll meet with circle(cylinder) at two points(lines). Since a red dot(line) is always closer than a blue dot(line), sum of all forces will head to the left(?).

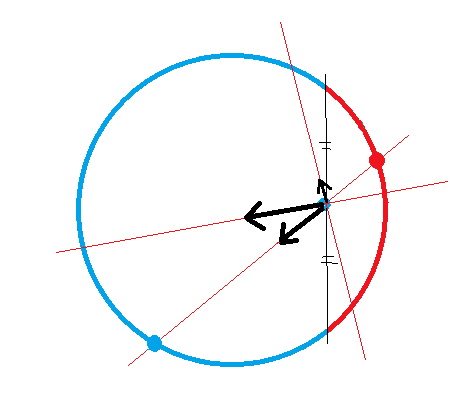
But this weird calculation conflicts with the fact that E=0 in the hollow of the cylinder.

What is a critical mistake of this logic(?). Will it be possible to explain why this image is wrong without using exact calculation?

 

[kuruman]

It is good that you worry about this. The critical mistake in the logic is this. Imagine two intersecting lines crossing at your off-center point. They define a blue arc ds_blue and a red arc ds_red. We make the ds arcs very small, not like in your figures, so that the contributions to the E-field from each arc are antiparallel and can be treated as contributions from lines of charge . The charge on each arc is proportional to ds, so that the magnitude of its contribution to the E-field is $$ dE \sim \frac{ds}{r} = \frac{r d \theta}{r} = d \theta $$ Since the subtended angle by the two arcs is the same, the fields cancel. This argument is similar to the 3d argument for the electric field inside a uniformly charged shell, except there one uses solid angles.

 

[TwoEG]

It is good that you worry about this. The critical mistake in the logic is this. Imagine two intersecting lines crossing at your off-center point. They define a blue arc ds_blue and a red arc ds_red. We make the ds arcs very small, not like in your figures, so that the contributions to the E-field from each arc are antiparallel and can be treated as contributions from lines of charge . The charge on each arc is proportional to ds, so that the magnitude of its contribution to the E-field is $$ dE \sim \frac{ds}{r} = \frac{r d \theta}{r} = d \theta $$ Since the subtended angle by the two arcs is the same, the fields cancel. This argument is similar to the 3d argument for the electric field inside a uniformly charged shell, except there one uses solid angles.

Thanks for cool explanation! They are canceling out each other so clearly... awesome!