Albert1
- 1,221
- 0
HI : good to see you everybody ,I am a new comer on this board
Being a math teacher ,I always trained my students with various difficult problems
from now on I am going to post a sequential challenging questions for people to share
most of them I know the answer and the solution of it , maybe your solution is quicker and smarter (Yes)
please try it many thanks
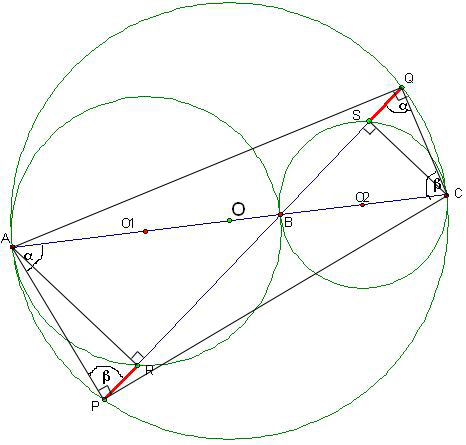
here comes the problem :

Being a math teacher ,I always trained my students with various difficult problems
from now on I am going to post a sequential challenging questions for people to share
most of them I know the answer and the solution of it , maybe your solution is quicker and smarter (Yes)
please try it many thanks
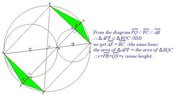
here comes the problem :

Last edited by a moderator: