Gbox
- 54
- 0
Moved from a technical forum
Summary: Finding state at t=0, energy values and more

So this is my first question in quantum mechanics (please understand).
1. So we have a system, and to describe the state of the system we have to measure, A is an hermitian matrix, that each physical measurable quantity has.
To find the state after the measurement we first need to find the eigenvectors of A which are for λ1 = 0.5 v1=1/sqrt(2)(1 , 1) and for λ2 = 1.5 v1=1/sqrt(2)(-1 , 1)
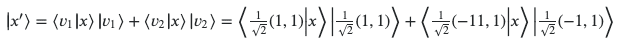
Now we have to normalize the vector, but because the eigenvalues are non degenerate we know that
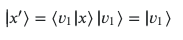
So
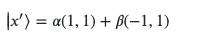
As it the superposition of the two states.
2. what are energy values? are they the eigenvalues?
So this is my first question in quantum mechanics (please understand).
1. So we have a system, and to describe the state of the system we have to measure, A is an hermitian matrix, that each physical measurable quantity has.
To find the state after the measurement we first need to find the eigenvectors of A which are for λ1 = 0.5 v1=1/sqrt(2)(1 , 1) and for λ2 = 1.5 v1=1/sqrt(2)(-1 , 1)
Now we have to normalize the vector, but because the eigenvalues are non degenerate we know that
So
As it the superposition of the two states.
2. what are energy values? are they the eigenvalues?