binbagsss
- 1,291
- 12
-See attached diagram
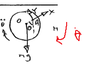
- A uniform disc of mass m and radius a is free to rotate in a vertical plane about a fixed smooth horizontal axis, the axis passes through the mp A of the radius of the disc.
- It then asks you to dervie equations of motion for when AO makes an angle pheta with the downward vertical ( and to find the force perpendicular to AO when AO is in this position)
To get the correct solution, the diagram needs to be correct - if I'm correct, as this determines whether the mass is speeding up or down, as if the angle was on the opposite side, the mass would INSTEAD be speeding up - which changes everything.
I have a few questions in how exactly the question specifies some details of the diagram
1) The angle with the downward vertical, why is it not the other side - is this convention, as in when they specify pheta with the downward vertical it is the counter clockwise direction.
2) Why is the angular acceleration not negative - as the body slows down as it goes upward.(Actually, I assume this is relative to the equation itself, as if you did this, you would get the same for Y , taking mg as negative)
3) To the diagram I have added a direction for the angular velocity - is this correct? Also if you choose to do this, shouldn't the angular acceleration be drawn in the opposite direction?
- A uniform disc of mass m and radius a is free to rotate in a vertical plane about a fixed smooth horizontal axis, the axis passes through the mp A of the radius of the disc.
- It then asks you to dervie equations of motion for when AO makes an angle pheta with the downward vertical ( and to find the force perpendicular to AO when AO is in this position)
To get the correct solution, the diagram needs to be correct - if I'm correct, as this determines whether the mass is speeding up or down, as if the angle was on the opposite side, the mass would INSTEAD be speeding up - which changes everything.
I have a few questions in how exactly the question specifies some details of the diagram
1) The angle with the downward vertical, why is it not the other side - is this convention, as in when they specify pheta with the downward vertical it is the counter clockwise direction.
2) Why is the angular acceleration not negative - as the body slows down as it goes upward.(Actually, I assume this is relative to the equation itself, as if you did this, you would get the same for Y , taking mg as negative)
3) To the diagram I have added a direction for the angular velocity - is this correct? Also if you choose to do this, shouldn't the angular acceleration be drawn in the opposite direction?