IronHamster
- 28
- 0
In the double slit experiment, a wave is forced to go through a tiny slit. I do not understand what is stopping it from going through the barrier.
After all, we can think of an electromagnetic wave as just the electric/magnetic fields of a sinusoidally oscillating particle, evaluated using the retarded position and time of that particle. Coulomb's Law and Biot-Savart say nothing of what is between the particle and the point in space its force is acting on--they work regardless, right?
In other words, why doesn't the wave simply pass through the barrier? Why don't we see this:
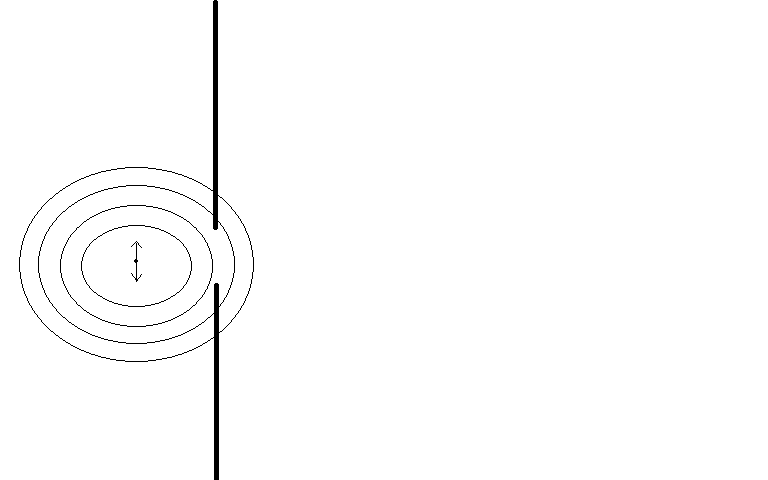
After all, we can think of an electromagnetic wave as just the electric/magnetic fields of a sinusoidally oscillating particle, evaluated using the retarded position and time of that particle. Coulomb's Law and Biot-Savart say nothing of what is between the particle and the point in space its force is acting on--they work regardless, right?
In other words, why doesn't the wave simply pass through the barrier? Why don't we see this: