Engineering What Determines the Resonant Frequency in a Series RLC Circuit?

Click For Summary
SUMMARY

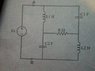
The resonant frequency in a series RLC circuit is determined by the formula w0 = 1/sqrt(LC), where L is the inductance and C is the capacitance. To analyze the circuit, one must calculate the equivalent impedance Z using the equations z = R + jwL + 1/jwC and apply Kirchhoff's Current Law (KCL) to derive the necessary relationships. The discussion emphasizes the importance of understanding the behavior of inductors and capacitors at DC and high frequencies to simplify the analysis. Additionally, the quality factor Q is defined as Q = w0L/R, which plays a crucial role in determining the bandwidth of the circuit.

PREREQUISITES
  • Understanding of series RLC circuit theory
  • Familiarity with complex impedance calculations
  • Knowledge of Kirchhoff's Current Law (KCL)
  • Basic concepts of resonant frequency and quality factor (Q)
NEXT STEPS
  • Study the derivation of the resonant frequency in RLC circuits
  • Learn how to apply Kirchhoff's Current Law (KCL) in circuit analysis
  • Explore the effects of varying frequency on the impedance of inductors and capacitors
  • Investigate the concept of quality factor (Q) and its implications in circuit design
USEFUL FOR

Electrical engineering students, circuit designers, and anyone involved in analyzing or designing RLC circuits will benefit from this discussion.

neiks997
Messages
3
Reaction score
0

Homework Statement


I will give a circuit of 5 passive components and an AC voltage source producing a sinusoidal voltage at a fixed frequency of omega / (2*pi) Hz.
i will post a picture asking what is being looked for along with the circuit.

Homework Equations


z = R + jwL + 1 / jwc, jw0L + 1 / jw0c = 0, w0 = 1/ sqrt(LC), B = w2 - w1 = R/L = w0/Q, Q = w0L / R = 1/w0RC, w1 = w0 - B/2, w2 = w0 + B/2


The Attempt at a Solution


clueless on how to make an equivalent circuit.
 

Attachments

  • 487198_10151160914350829_1701334509_n.jpg
    487198_10151160914350829_1701334509_n.jpg
    55.4 KB · Views: 532
  • 552270_10151160913580829_1935626978_n.jpg
    552270_10151160913580829_1935626978_n.jpg
    73.4 KB · Views: 503
Physics news on Phys.org
neiks997 said:

Homework Statement


I will give a circuit of 5 passive components and an AC voltage source producing a sinusoidal voltage at a fixed frequency of omega / (2*pi) Hz.
i will post a picture asking what is being looked for along with the circuit.

Homework Equations


z = R + jwL + 1 / jwc, jw0L + 1 / jw0c = 0, w0 = 1/ sqrt(LC), B = w2 - w1 = R/L = w0/Q, Q = w0L / R = 1/w0RC, w1 = w0 - B/2, w2 = w0 + B/2


The Attempt at a Solution


clueless on how to make an equivalent circuit.

Welcome to the PF.

It says it wants you to find the equivalent circuit impedance Z that is formed by those components in that configuration.

There are no obvious simplifications of the circuit, so you need to write the KCL equations for the circuit, to find the Z = Vin/Iin impedance. Use the complex impedances for the L and C components...
 
none of the capacitors or inductors are in parallel or series with each other?
 
neiks997 said:
none of the capacitors or inductors are in parallel or series with each other?

Nope. That's why you need to write the KCL equations to solve this.
 
I'd be tempted to do parts 2 and 3 first. What happens to L's and C's at DC and very high frequencies?

It's been many years since I did this but I half remember a trick that relies on the impedance of the source being low to simplify the circuit?
 
CWatters said:
I'd be tempted to do parts 2 and 3 first. What happens to L's and C's at DC and very high frequencies?

It's been many years since I did this but I half remember a trick that relies on the impedance of the source being low to simplify the circuit?

brilliant
 

Similar threads

Series RLC Circuits: Resonant Frequency of 60° at 40 Hz
  • · Replies 8 ·
Replies
8
Views
3K
About the definition of resonance frequency
  • · Replies 40 ·
2
Replies
40
Views
6K
Resonant frequency of L - R||C circuit
  • · Replies 21 ·
Replies
21
Views
1K
Engineering How Do You Calculate iC(t) in an RLC Circuit and Plot Its Waveform?
  • · Replies 3 ·
Replies
3
Views
4K
Engineering Finding values of RLC circuit given resonance frequency
  • · Replies 6 ·
Replies
6
Views
4K
Engineering How to Determine iL(t) in a Series RLC Circuit with Switching?
  • · Replies 7 ·
Replies
7
Views
6K
How do I determine the resistance for RLC low pass filter?
  • · Replies 4 ·
Replies
4
Views
774
Engineering Amplified Tuner Circuit, Finding Resonant Frequency
  • · Replies 3 ·
Replies
3
Views
2K
Determine resonant frequency of an AC voltage source
  • · Replies 6 ·
Replies
6
Views
4K
Engineering RLC circuit and resonance frequency
  • · Replies 5 ·
Replies
5
Views
4K