Amplified Tuner Circuit, Finding Resonant Frequency

[liamporter1702]

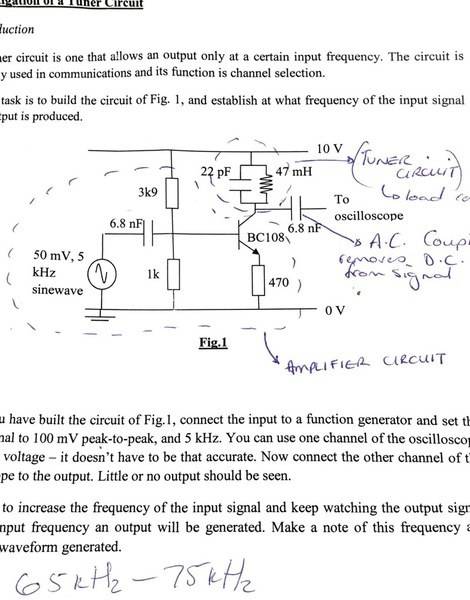
I am looking to find the resonant frequency of the amplified tuner circuit below
The equation I have attempted to use is the f = 1/2*pi*√LC
With the values for the inductance capacitance being 22pF and 47mH as I believe this is the tuner part of the circuit?
The value I get by inserting these values is 156.5kHz.
But from doing a practical experiment using this circuit I know the resonant frequency is somewhere between 65kHz and 75kHz. Can faulty equipment be to blame for such a difference in values? Or is there a specific equation to be used for amplified tuner circuits?
Thanks for any help!

 

[gneill]

Do you have any details about the impedance of the oscilloscope and the probe used? Along with the output coupling capacitor they will represent another tuned circuit in parallel with the intended load (LC tank). A typical oscilloscope's input impedance might be represented by 1 MegOhm in parallel with around 10 or 15 pF. A probe and its cable will modify that.

Do you have details on the tank component tolerances? Are they 1% parts? 10%?

For high frequencies, circuit layout and construction can become important. Stray capacitance might affect your tank's resonant frequency if leads are long or carelessly arranged near other parts or metal objects.

Your 156 kHz value should be correct for the given tank circuit. I'm guessing that oscilloscope loading and moderate stray capacitance might pull the net resonant frequency downwards a bit, maybe closer to 120 kHz if things are bad. 75 kHz seems a bit of a stretch.

I note that your 75 kHz is about half the expected frequency. How did the signal shapes look on the oscilloscope? Any sign of clipping or other non-linearity? Clipping might introduce a 2nd harmonic that the tank is responding to.

 

[rude man]

22pF is a VERY small capacitance. I agree with gneill that parasitic capacitance is probably a factor here.
But beyond that, combining such a small C with such a large L is problematic in itself. In fact, the interwinding capacitance of your coil is probably beyond 22 pF, and the self-resonant frequency is probably close to your calculated 150 kHz. This means that your coil looks like a resistor, not a coil, throwing calculations off badly.

I suggest a redesign if you want 150 kHz resonance: 2200 pF and 0.47 mH.

 

[liamporter1702]

Sorry this was part of a university experiment so I don't have any values for oscilloscope impedance and the probes I used, I'm in my first year so I'm still learning, these values now seem like a good idea to ask for hahaa.

I wouldn't say leads were particularly long or carelessly arranged, but this may be part of the problem.

I have attached a picture of the waveforms I obtained from my circuit but clipping does not seem to be a problem to me.

I also simulated the circuit in Proteus and that seems to give 150kHz as well, so that probably means its something to do with the components I'm assuming?

Thanks rude man for the explanation, I think I may suggest a redesign as part of my work!