Discussion Overview
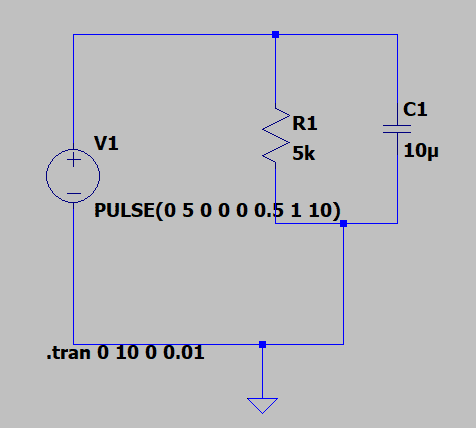
The discussion revolves around the determination of the time constant in a parallel resistor-capacitor (R-C) circuit. Participants explore the implications of circuit configurations, the role of series resistance, and the mathematical analysis required to understand the charging and discharging behavior of the capacitor.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants assert that the initial connection of the capacitor across an ideal voltage source is problematic due to the absence of series resistance, which could lead to unrealistic current values during transitions.
- Others propose that every voltage source and capacitor has some finite series resistance that must be considered for accurate modeling.
- A participant suggests that the time constant for charging the capacitor is calculated using the formula R1*C1, but others challenge this by noting the presence of multiple resistors affecting the time constant.
- Some participants recommend using Kirchhoff's Current Law (KCL) equations to derive the actual time constant, while others advocate for Thevenin's theorem as a simpler alternative.
- There is a discussion about the importance of understanding idealized components versus real-world components, highlighting that simplifications can lead to misleading results.
- A participant expresses difficulty in solving the integral equation for current in the circuit, indicating the complexity of the analysis required.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the correct approach to determine the time constant, with multiple competing views on the significance of series resistance and the appropriate mathematical methods to use.
Contextual Notes
Limitations include the potential for missing assumptions regarding series resistance and the complexity of the circuit analysis, which may lead to different interpretations of the time constant based on the chosen method.