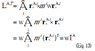What Do Symbols in Angular Dynamics Equations Represent?

[Nanako]

Angular dynamics: Help Needed

hi everyone! I'm trying to learn angular dynamics from this document: http://chrishecker.com/images/c/c2/Gdmphys2.pdf

I believe I'm understanding it all pretty well so far, but i come to a stumbling block when it's time to learn about total angular momentum, and the moment of inertia. i don't fully understand the two equations being used to teach these areas.

I'm wondering if someone could help by picking them apart and explaining what each symbol means, and how it fits together.

The equations in question are eq 12 and 13 in the above document. For simplicity i'll post pictures of them here too

Firstly:

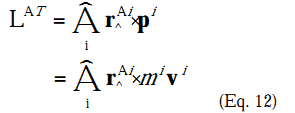
I believe this one is designed to show a simple, but slow way of calculating total linear momentum.

There are two main things i don't understand:
Firstly, the giant A with the hat on it and the symbol underneath. I've got almost no idea what this means, other than that it relates to point A on a diagram in the document. it might be a unit vector? but why does it have a variable underneath it in subscript, and why is it overly large.

secondly, i
No point i is mentioned anywhere until now, so I'm guessing it means some sort of mathematical symbol I'm not aware of. index i think, but I'm not sure what that means in this context or how it relates to this equation.

i understand the rest pretty well. dot product of perpendicularised r and p

Secondly:

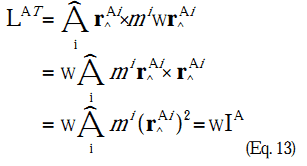
This is built out of the first equation, and it loses me a bit with the introduction of angular acceleration. I believe it shows how to calculate the moment of inertia, but that's a concept I'm still trying to wrap my head around.

My best understanding of the moment of inertia is that it's a threshold of torque needed to cause a change in an object's angular acceleration/velocity. I'm not sure that's quite right though.



Clearly there's some holes in my knowledge, and the explanations written here aren't quite doing it for me. Can anyone help better explain what is going on here? x

 

[jfizzix]

For starters, I would not learn physics from a document whose notation is so confusing. I'm a grad student who's TA-ed classical mechanics a few times, and the notation you use is news to me.

However, the ideas are quite simple.

First: The total angular momentum is just the sum of the angular momentum of all the individual parts. The same is true for linear momentum, and energy, and a lot of other things in physics.

Second: Because there is no preferred origin of coordinates, you can always break up the total angular momentum into two terms. The angular momentum of the center of mass \vec{L}_{orbit}=\vec{r}_{CM}\times \vec{p}_{CM}, and the angular momentum with respect to the center of mass \vec{L}_{spin}=\bar{I}\cdot \vec{\omega}_{CM}, so that \vec{L}=\vec{L}_{orbit}+\vec{L}_{spin}. Many times, we're in a reference frame where the center of mass is stationary, so that \vec{p}_{CM}=0, but the object might still be spinning, so you just have \vec{L}=\bar{I}\cdot \vec{\omega}_{CM}, but you can always think of the total as the sum of both orbital and spin parts.

Maybe this didn't answer your question, but I hope it helps:)

 

[jfizzix]

here the moment of intetia \bar{I} is considered to be with respect to the center of mass. I thought I'd clear that up since you can calculate the moment of inertia with respect to any origin.