What Does Zee Mean by the Equation in QFT Nut, III.6, p. 194?

[Lapidus]

..where can be found:

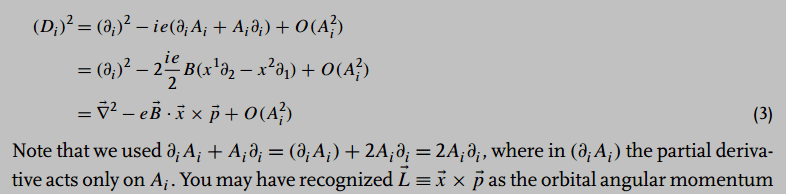
What in the whole wide world does Zee mean with

??

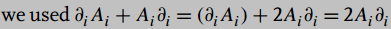Thank you

 

[DrDu]

I guess that $(\partial_i A_i)$is another way to say div A, which probably vanishes in the gauge Zee is considering. The bracket probably means that the action of the partial derivative is restricted to A.

 

[Lapidus]

But on what else could the partial derivative act on than on A?

 

[DrDu]

On what does it act in $A_i \partial_i$? I mean, you are considering a momentum operator, so it will act on some wavefunction, besides A.

 

[mfb]

A better way to write this would be
$$(\partial_i A_i + A_i \partial_i) X = (\partial_i A_i)X + 2 A_i \partial_i X = 2 A_i \partial_i X$$
for some wave function X and ignoring indices there. Just the product rule applied to $\partial_i A_i X$

Edit: Added missing X

 

[Lapidus]

Got it! Thanks DrDu and mfb!

 

[vanhees71]

This book by Zee, although apparently written in a quite colloquial way, confuses (at least me) more than it helps. This is an example. Instead of writing the simple matter in a simple way as mfb did in #5 he only gives some short-hand notation, which is more confusing than helpful :-(.

 

[ChrisVer]

Well it's so and so; it seems like a bigger generalization of the derivation of $xp -px = i \hbar$. Without having to write $(xp - px ) f(x) = i \hbar f(x)$.
Although I think similar expressions were in Griffith's Intro to Electrodynamics.
(feels like Zee's advocate)

 

[nrqed]

A better way to write this would be
$$(\partial_i A_i + A_i \partial_i) X = (\partial_i A_i) + 2 A_i \partial_i X = 2 A_i \partial_i X$$
for some wave function X and ignoring indices there. Just the product rule applied to $\partial_i A_i X$

Just to point out a small misprint (mfb just forgot): there is an X missing in the middle expression$$(\partial_i A_i + A_i \partial_i) X = (\partial_i A_i) X + 2 A_i \partial_i X = 2 A_i \partial_i X$$