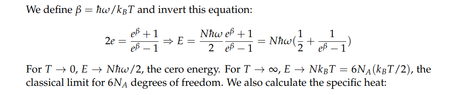What Happens to the Limit of This Function as T Approaches Infinity?

[Another1]

$$\lim_{{T}\to{\infty}}N \bar{h}\omega \left( \frac{1}{2} + \frac{1}{e^{\frac{ \bar{h}\omega}{k_BT}}-1} \right)$$
In term $$\lim_{{T}\to{\infty}}N \bar{h}\omega \left( \frac{1}{e^{\frac{ \bar{h}\omega}{k_BT}}-1} \right)=N \bar{h}\omega \lim_{{T}\to{\infty}}\left( \frac{1}{e^{\frac{ \bar{h}\omega}{k_BT}}-1} \right)$$
but $$\left( \frac{1}{e^{\frac{ \bar{h}\omega}{k_BT}}-1} \right)$$ in the form $$\frac{1}{0}$$
please give me a idea

View attachment 8741

 

[I like Serena]

Hi Another,

The expression for $E$ still has a $T$ in it when $T\to\infty$.
It means that we are looking for an oblique asymptote instead of a horizontal asymptote.
That is, if $T\to\infty$ we should find that $\pd E T\to Nk_B$, so that that we get the oblique asymptote $E\to Nk_BT$.

 

[Another1]

Hi Another,

The expression for $E$ still has a $T$ in it when $T\to\infty$.
It means that we are looking for an oblique asymptote instead of a horizontal asymptote.
That is, if $T\to\infty$ we should find that $\pd E T\to Nk_B$, so that that we get the oblique asymptote $E\to Nk_BT$.

I do not understand, please give an example to explain it?

why $\pd E T\to Nk_B$, ?

 

[I like Serena]

I do not understand, please give an example to explain it?

why $\pd E T\to Nk_B$, ?

Consider the function given by $f(x)=\frac 1x + x + 1$.
It has:
$$\lim_{x\to\infty} f(x) = \infty $$

[DESMOS]advanced: {"version":7,"graph":{"squareAxes":false,"viewport":{"xmin":-10,"ymin":-10,"xmax":10,"ymax":10}},"expressions":{"list":[{"type":"expression","id":"graph1","color":"#2d70b3","latex":"y=\\frac{1}{x}+x+1"},{"type":"expression","id":"2","color":"#388c46","latex":"y=x+1"}]}}[/DESMOS]
It also has the oblique asymptote $y=x+1$.
We can find its slope through the limit of $f'(x)$ when $x\to\infty$.
We have:
$$\lim_{x\to\infty} f'(x) =\lim_{x\to\infty} \left(-\frac{1}{x^2} + 1\right) = 1$$
Therefore the oblique asymptote exists and has slope $1$.
Put otherwise, when $x\to\infty$ we have that $f(x)\to x$.
Note that we didn't find the $y$-intercept yet, which we didn't need.