What Happens When Observers Approach an Event Horizon?

[Spin-Analyser]

I'm not sure why the other thread was locked, unless you're banning questions? I'll ask it in as clear a way as possible.


When an observer approaches an event horizon to one plank length away one of two things must happen:

1). Any observers previously falling towards the black hole would be right along side you.

2). There is distance between you and the light from previous in-falling observers when you're right on the horizon. That would mean you would have to be seeing light from inside the horizon, although it's light that hasn't reached the horizon yet, which is paradoxical because you can't tell if they crossed. How can you be hovering the same distance away from the horizon as a previous observer and have space between you?

Please define the parameters of the universe in which that's supposed to make sense.

I was told that if you decide at the last minute to brake and hover at a small fixed distance outside the event horizon, you see your partner's image slow down, red-shift and darken and never actually cross the horizon. But if you're right next to the horizon and you never see them cross the horizon then how can there be space between you?


Please don't lock or delete this thread. These are legit questions. I honestly don't think anyone's explained how an image can be coming from inside the horizon of an object that might not have crossed the horizon yet? This isn't "word soup", it's a fair question.

 

[Doc Al]

I'm not sure why the other thread was locked, unless you're banning questions?

The other thread (https://www.physicsforums.com/showthread.php?t=583903) was locked, not because you were asking questions, but because you were simply ignoring the answers and repeating the same thing. Don't let that happen here. Threads that simply go round in circles will be locked.

 

[Sam Gralla]

Point 1) is wrong, and I don't understand point 2). It all sounds very suspicious because you're talking about being "1 Planck length away". Classical physics (such as general relativity) is based on a continuous description of spacetime and you won't find any qualitatively different phenomena at any two different finite distances from the horizon. Of course, if you're saying GR isn't going to correctly describe physics within a Planck length, few will disagree with you.

 

[Naty1]

I don't believe this perspective was discussed in the prior [now locked] discussion:

http://en.wikipedia.org/wiki/Black_hole_complementarity

Leonard Susskind...also postulated a stretched horizon, which is a membrane hovering about a Planck length outside the event horizon and which is both physical and hot.

note to PeterDonis: This short article addresses your prior question we discussed in yet another thread about the 'no cloning theorem'. The explanation in Wiki confirms my recollection of what Susskind says in his BLACK HOLE WAR.

Spin:

"..I accept the concept that, as almost infinite energy is required to hover near the event horizon, gravity can be inferred to become infinite at the EH..."

from #67, PeterDonis:
""...Gravity" in the sense of "the proper acceleration required to hover at a constant radius". But there are other senses of "gravity" that are *not* infinite at the horizon, as several posters have pointed out. Curvature in the sense of the Riemann curvature tensor, for example, or various scalars derived from it, is perfectly finite at the horizon...

Conditions at or near a horizon are indeed 'weird'...contrary to our normal 'intuition'...Gravity IS the curvature of space and time...yet acceleration layers further curvature in addition to this 'spacetime curvature' of gravity...Peter's explanation is CRAZY...but I believe accurate!

I was told that if you decide at the last minute to brake and hover at a small fixed distance outside the event horizon, you see your partner's image slow down, red-shift and darken and never actually cross the horizon. But if you're right next to the horizon and you never see them cross the horizon then how can there be space between you?

you are assuming light approaches you 'normally' when it is in fact ..."takes a while (up to forever) to reach you...[PAllen]


I can see two issues perhaps 'fogging' your interpretation[one's we have all probbaly faced] : one is that you are perhaps not thinking very carefully about what has been posted, perhaps applying traditional intuition, [and this stuff is not easy to 'visualize] and secondly, it may not be clear which frame of reference is under discussion, sentence by sentence.

For example when you wrote:

You're saying you can observe light coming out to your eye from inside the horizon as you hover just above it ...

I thought "oh boy" nobody said THAT! A hovering observer is causally disconnected from all events INSIDE the horizon...while a free falling observer, in sharp contrast, can 'see inside'...if those two observers pass each other they observe very different things and, for example, time passes very differently for them. It's analogous, if not identical, to an Unruh [accelerated] observer making different observations than an inertial observer.


As an impartial observer, I don't think you'll get any clearer explanations than were provided in the prior discussion...but don't expect they will all make immediate 'intuitive sense'...you have to think differently as a result of what the mathematics reveals. Have you considered rereading that last thread? You should not expect immediate clarity the first time you read some of these perspectives. I have sometimes have to read four or five times before the 'light goes on'...

What I also found useful was writing down some 'principles' which I would accept and begin my reasoning from there...
like maybe "everything is relative...everything is frame dependent" and refining it near balck hole horizons to "A free falling observer sees no horizon, a hovering observer is fried [cooked] by it..."
and refining my understanding from there...

 

[Naty1]

Sorry, the above post got too long...

Spin:

But if you're right next to the horizon and you never see them cross the horizon then how can there be space between you?

Maybe it would be clearer if you thought of spaceTIME instead of space?...


Peter #33:

If you are orbiting the black hole at some radial coordinate r outside the horizon, you will see the effective mass of the black hole increase as soon as the infalling object falls inside your radius. (Strictly speaking, this is what you will see if the infalling object falls right by you on its way in; i.e., if its angular coordinates theta, phi are exactly the same as yours. If it falls at some other theta, phi, it may take time for the effect to propagate to you before you actually see an increase in mass.)

PAllen #82

"So if you are close enough to the horizon you can observe objects crossing it?"

This is getting repetitive. You are seeing an old image from before they crossed. It is from when they were still (in my prior example) 10 feet from you but right near the horizon. This light takes a while (up to forever) to reach you.

 

[PAllen]

from #67, PeterDonis:
""...Gravity" in the sense of "the proper acceleration required to hover at a constant radius". But there are other senses of "gravity" that are *not* infinite at the horizon, as several posters have pointed out. Curvature in the sense of the Riemann curvature tensor, for example, or various scalars derived from it, is perfectly finite at the horizon...

Conditions at or near a horizon are indeed 'weird'...contrary to our normal 'intuition'...Gravity IS the curvature of space and time...yet acceleration layers further curvature in addition to this 'spacetime curvature' of gravity...Peter's explanation is CRAZY...but I believe accurate!

Not only accurate, but it need not be mysterious at all. There is an equivalent Newtonian analog to this:

Imagine you are on the surface of a planet enormous radius with enormous mass. The acceleration you will need to hover just above the surface will be enormous. Tidal forces will be small (because radius is enormous). The acceleration is due to depth of gravitational well - a global feature. The tidal forces due to gradient - a local feature.

The GR analog is conceptually similar. Curvature per se is local and corresponds roughly to tidal gravity. Very roughly, you can imagine the proper acceleration aspect of gravity as reflecting accumulated difference in geometry between near horizon and flat spacetime at infinity. More specifically, you can say that an (r,theta,phi)=constant world line is geodesic at infinity, but diverges ever more from the local geodesic as you approach the horizon.

 

[yuiop]

When an observer approaches an event horizon to one plank length away one of two things must happen:

1). Any observers previously falling towards the black hole would be right along side you.

If previous falling observers are "right alongside you" then they are exactly one Planck length away from the EH and therefore did not fall earlier but simultaneously. The sentence is a self contradiction. (Perhaps the letters got mixed up when you stirred the soup? ...hehe :P ) Previously falling observers will be less than a plank distance away from the EH. Of course you might be assuming that there cannot be a distance of less than one Plank length but that is unproven and unlikely and you seem to assuming that we are living in a spatially digital universe. Also bear in mind that due to gravitational length contraction (for want of a better term) what we call one Planck length from a coordinate point of view might well be measured as a distance of several Kilometers from the point of view of local observers. Where do we define the Planck length? Locally or in coordinate terms?

Also bear in mind you cannot see light emitted from inside the EH or even exactly at the EH. even if you one Planck length outside the EH.

2). There is distance between you and the light from previous in-falling observers when you're right on the horizon. That would mean you would have to be seeing light from inside the horizon, although it's light that hasn't reached the horizon yet, which is paradoxical because you can't tell if they crossed. How can you be hovering the same distance away from the horizon as a previous observer and have space between you?

This is looking soupy too. You said you are "right on the horizon" which to most people would mean you are exactly zero Plank lengths from the horizon but then you say you are hovering the same distance away from the horizon. If you are hovering you cannot be exactly zero Planck lengths away from the horizon so again you are contradicting yourself. Are you on the horizon on just outside it? You seem to be using one Planck length to mean a finite non zero quantity sometimes and at other times pretending that one Plank length is as good as zero, when in reality they are worlds apart. It is similar to saying that traveling at 99.9999999999% of the speed of light is as good as traveling at the the speed of light when they are worlds apart.

But if you're right next to the horizon and you never see them cross the horizon then how can there be space between you?

More soup. By "right next to the horizon" do you mean right on the horizon or do you mean some distance away from the horizon? If you are some small but non zero distance away from the horizon then by definition there is space between you and the horizon and also space between you and the previously infalling observer. If you mean you are zero Planck lengths away from the horizon (i.e. right on the horizon) then you can see light from other objects that fell through the horizon.

The only time you can see light from objects that see inside the horizon or exactly on the horizon is when you are also exactly on the horizon or below it. Even hovering one Planck length outside the horizon, you never see anything arrive exactly at the horizon. All you see are gradually red shifting, dimming but persistent ghostly images that become undetectable before they cross.

 

[yuiop]

A hovering observer is causally disconnected from all events INSIDE the horizon...while a free falling observer, in sharp contrast, can 'see inside'...if those two observers pass each other they observe very different things and, for example, time passes very differently for them.

This is potentially confusing to the the OP and perhaps fuelling the fire.

You should perhaps stress that a free falling observer can "see inside" if and only if the free falling observer is at the event horizon or has passed through the event horizon.

They might see different things such as the degree of red shift but what they have in common is that neither of them see inside the EH while outside the EH.

 

[PeterDonis]

note to PeterDonis: This short article addresses your prior question we discussed in yet another thread about the 'no cloning theorem'. The explanation in Wiki confirms my recollection of what Susskind says in his BLACK HOLE WAR.

Yes, what's on that wiki page seems consistent with what I remember of Susskind's The Black Hole War as well. His way of getting around the no-cloning theorem is basically to say that no single observer will ever see both "copies" of the information, so it's OK.

The claim that no observer can see both copies, in and of itself, seems correct to me because once you're inside the horizon, not only can you never get back out, but you can't even "hover" at a constant distance from the singularity--you will inevitably reach the singularity and any information you carry will be destroyed there along with you; even light rays can't "hover" at a constant distance from the singularity any more, so they will also be sucked into the singularity and destroyed.

This does seem like a lot of quirky claims in QM--yes, this can in principle happen, but nobody will ever see it, so it's doesn't violate the rules. Kind of like EPR experiments show that nonlocal correlations can be mediated faster than light, but no actual information can ever be exchanged that way, so it's OK. Einstein would probably be tearing his hair if he were still around to read Susskind's book.

 

[PeterDonis]

When an observer approaches an event horizon to one plank length away one of two things must happen:

1). Any observers previously falling towards the black hole would be right along side you.

2). There is distance between you and the light from previous in-falling observers when you're right on the horizon. That would mean you would have to be seeing light from inside the horizon, although it's light that hasn't reached the horizon yet, which is paradoxical because you can't tell if they crossed. How can you be hovering the same distance away from the horizon as a previous observer and have space between you?

First, please note that Sam Gralla's comments are correct: if we are talking about classical GR, there is no "minimum distance" that something can be above the horizon, so the Planck length is irrelevant; above the horizon is above the horizon. Everything I say in what follows will assume that the questions above have been modified appropriately.

There's a model of Schwarzschild black holes that might be helpful in visualizing how all this works: the "river model" of black holes. See this paper:

http://arxiv.org/abs/gr-qc/0411060

Basically, the idea is that space is flowing inward into the black hole's singularity; at any given radius r, the rate at which space flows inward is the "escape velocity" at that radius. So space is like a "river" that continually flows inward, carrying things along with it.

If you are free-falling into the hole, you are basically at rest in the river, so you are moving inward at the same rate the river is. So suppose you are free-falling inward, and you have a blinker below you that sends repeated flashes of light back up to you. The blinker is attached to you so it stays at the same physical distance from you; we assume that the hole is large enough that tidal gravity is negligible until you are almost at the singularity, so the blinker can remain attached to you safely. The light from the blinker is moving "against the stream", so to speak, at the speed of light--that is, it moves outward at the speed of light *relative to the river*.

But relative to the "river bed", that is, relative to observers "hovering" at rest at a constant radius r, the light moves outward *more slowly* as you get closer to the hole (because the river flows inward faster). At the horizon, the river is flowing inward at the speed of light, so outgoing light is just able to cancel out the flow and remain at the same radius, the horizon radius, forever. Inside the horizon, the river is flowing inward faster than light (this is OK because the "river bed" doesn't actually exist physically, it's just an aid to visualization), so even outgoing light rays are dragged inward (just more slowly than anything else in the river).

Now consider flashes of light emitted by the blinker at various points as you fall. To you, they all look the same: they rise toward you at the speed of light, and take the same time (relative to your clock) to reach you. However:

(1) A flash emitted far away from the hole will be moving outward, relative to the river bed, at almost the speed of light (since the river is flowing inward very slowly). So an observer "hovering" at rest relative to the river bed will see things pretty much the same way you do.

(2) A flash emitted when you are getting fairly close to the hole will be moving outward, relative to the river bed, somewhat slower than the speed of light (since the river is now flowing inward at an appreciable fraction of the speed of light). So the observer will see the light rise more slowly than you do; to him, it will look as if you are falling to meet the light, to some extent, rather than the light rising to you.

(3) A flash emitted when the blinker is just above the horizon will be moving outward *very* slowly; and you yourself will be falling, relative to the river bed, at almost the speed of light. So to an observer "hovering" at rest there, the light hardly seems to move at all; instead, you fall to meet it at a point just slightly above the point where it was emitted, relative to the river bed. In fact, if the flash is emitted close enough to the horizon, the blinker itself might actually be *below* the horizon by the time you have fallen to meet the flash of light.

(4) A flash emitted when the blinker is exactly *at* the horizon stays at the horizon; as noted above, the outward speed of the light at the horizon just cancels the inward speed of the river, so the light stays at the same place relative to the river bed. So you will see the flash exactly when you, yourself, cross the horizon. By that time, though, the blinker will have fallen below the horizon; the blinker itself does not "wait" at the horizon for you, only the flash it emitted at the horizon does. So the blinker will not be "next to you" when you cross the horizon; it will be further inward, just as it is throughout your fall.

(5) A flash emitted when the blinker is below the horizon moves *inward*, relative to the river bed, even though it is emitted outward; as noted above, even outgoing light is dragged inward in the region below the horizon. But the outgoing light is dragged inward more slowly than you are, since you are moving with the river; so you will still catch up to each light flash emitted by the blinker. When you do catch up to each flash, the blinker will have fallen further than it was when it emitted the flash, since it is also moving inward faster than the outgoing light is.

 

[yuiop]

The trouble with the river analogy is that it suggests that to a stationary observer hovering just outside the EH, up going light will be almost stationary and down going light will be traveling at almost twice the speed of light. In reality such a local observer see both up going light and down going light traveling at exactly the normal speed of light. The river model does not seem very good to me or I am missing the point somewhere.

 

[PAllen]

The trouble with the river analogy is that it suggests that to a stationary observer hovering just outside the EH, up going light will be almost stationary and down going light will be traveling at almost twice the speed of light. In reality such a local observer see both up going light and down going light traveling at exactly the normal speed of light. The river model does not seem very good to me or I am missing the point somewhere.

Actually, a near horizon hovering observer is extremely non-inertial, and there is no expectation of light speed isotropy for such an observer (as there is for a free falling observer). In a thread here, I think about a year ago, Passionflower presented rigorous calculation that such an observer measuring light speed over a finite distance (rather than infinitesimal) will, indeed, measure a difference in upward versus downward speed. There was even anisotropy in two way light speed for sucn an observer over finite distances.

 

[yuiop]

Actually, a near horizon hovering observer is extremely non-inertial, and there is no expectation if light speed isotropy for such an observer (as there is for a free falling observer). In a thread here, I think about a year ago, Passionflower presented rigorous calculation that such an observer measuring light speed over a finite distance (rather than infinitesimal) will, indeed, measure a difference in upward versus downward speed. There was even anisotropy in two way light speed for sucn an observer over finite distances.

I was initially using the infinitesimal assumption. However I disagree with the assertion that the upward speed of light differs from the downward speed of light over the same distance at the same location. Let me make this clearer. Consider the case of an observer with a mirror one metre below him and another ruler one metre above him. He finds that the time for a light signal to make the two way trip (down then up) to the mirror below him takes longer than the two trip way trip (up then down) to the mirror above him. Note that these are two way trips and so say nothing about the difference between upgoing light and down going light. Another difficulty is in how we define a metre. A metre is officially defined in terms of light speed or wavelength. If there is a difference in the time time to the lower mirror and back and to the upper mirror and back then we have to conclude that the mirrors are a metre above and below and have to adjust them until their times are equal. If we are more fussy then we can measure circumferences and divide by 2 Pi to get the radius and this will result in a different definition of the metre from the international CGPM definition and an anisotropic result will be obtained but all this tells us is that the speed of light lower down is slower than the speed of light higher up.

Now we can alter the experiment so that the we have a single ruler. Initially we have a source and clock at the bottom and a mirror at the top and record the two way time (up then down). Next we place the clock and source at the top and the mirror at the bottom and record this two way time (down then up). We note that we obtain different times. We also note that the light paths are exactly the same (only differing in order) and by symmetry arguments we conclude that the anisotropy in times is purely due to differences in time dilation on the clock depending upon whether they are placed at the top or bottom. None of these experiments say anything about differences in the one way speed of light going up or down, only that light speed id slower lower down (in either direction) than it is higher up.

OK, now we attempt to measure the one way speed (up or down) over the same vertical distance. First difficulty is synchronising the clocks which is a problem because we know clocks higher up run faster than clocks lower down. We can speed up the lower clock so that it runs at the same rate as the upper clock. Now we still have the standard difficulty that synchronising clocks requires we make certain assumptions about the one way speed of light in the first place so any conclusions are subject to circular reasoning. We cannot measure the one way speed of light in GR any more than we can measure the one way speed of light in SR for very similar reasons.

If we look at the Schwarzschild metric we can easily calculate that the vertical speed of light is the exactly the same going up or going down at a given radial coordinate. I can only assume that what Passionflower actually calculated was an anisotropy between the speed of light lower down compared to the speed of light higher up which can indeed be measure over finite local distances. I am pretty sure the calculation said nothing about an anisotropy between the up going one way speed of light and the down going one way speed of light over the same finite vertical distance.

 

[PAllen]

I was initially using the infinitesimal assumption. However I disagree with the assertion that the upward speed of light differs from the downward speed of light over the same distance at the same location. Let me make this clearer. Consider the case of an observer with a mirror one metre below him and another ruler one metre above him. He finds that the time for a light signal to make the two way trip (down then up) to the mirror below him takes longer than the two trip way trip (up then down) to the mirror above him. Note that these are two way trips and so say nothing about the difference between upgoing light and down going light. Another difficulty is in how we define a metre. A metre is officially defined in terms of light speed or wavelength. If there is a difference in the time time to the lower mirror and back and to the upper mirror and back then we have to conclude that the mirrors are a metre above and below and have to adjust them until their times are equal. If we are more fussy then we can measure circumferences and divide by 2 Pi to get the radius and this will result in a different definition of the metre from the international CGPM definition and an anisotropic result will be obtained but all this tells us is that the speed of light lower down is slower than the speed of light higher up.

Now we can alter the experiment so that the we have a single ruler. Initially we have a source and clock at the bottom and a mirror at the top and record the two way time (up then down). Next we place the clock and source at the top and the mirror at the bottom and record this two way time (down then up). We note that we obtain different times. We also note that the light paths are exactly the same (only differing in order) and by symmetry arguments we conclude that the anisotropy in times is purely due to differences in time dilation on the clock depending upon whether they are placed at the top or bottom. None of these experiments say anything about differences in the one way speed of light going up or down, only that light speed id slower lower down (in either direction) than it is higher up.

OK, now we attempt to measure the one way speed (up or down) over the same vertical distance. First difficulty is synchronising the clocks which is a problem because we know clocks higher up run faster than clocks lower down. We can speed up the lower clock so that it runs at the same rate as the upper clock. Now we still have the standard difficulty that synchronising clocks requires we make certain assumptions about the one way speed of light in the first place so any conclusions are subject to circular reasoning. We cannot measure the one way speed of light in GR any more than we can measure the one way speed of light in SR for very similar reasons.

If we look at the Schwarzschild metric we can easily calculate that the vertical speed of light is the exactly the same going up or going down at a given radial coordinate. I can only assume that what Passionflower actually calculated was an anisotropy between the speed of light lower down compared to the speed of light higher up which can indeed be measure over finite local distances. I am pretty sure the calculation said nothing about an anisotropy between the up going one way speed of light and the down going one way speed of light over the same finite vertical distance.

You have to adopt some conventions. Fermi-Normal coordinates say you use spacelike hypersurfaces 4-orthogonal to an observer's world line. Time, anywhere on each such surface is taken to be proper time along the time axis world line. Distances are proper lengths in the surfaces. Then, using this synch convention, you can define a one way light speed for such a non-inertial observer. There is no general expectation it is c, nor that it has any particular isotropies. In SC, it is trivial to compute that for a hovering observer, such a surface restricted to (r,t) is simply constant r. That is, unit vector in r direction is always 4-orthogonal to unit vector in t direction in SC geometry.

However, reviewing the calculation I see that I mis-remembered, and it is clear that up an down speed between r and r+h (for r taken as observer coordinates) will be the same. This is, in fact, obvious due to SC geometry being static (therefore time symmetric). What is true is that two way speed away from the horizon is different from two way speed toward the horizon, measured over any finite distance, for a hovering observer.

 

[PeterDonis]

The trouble with the river analogy is that it suggests that to a stationary observer hovering just outside the EH, up going light will be almost stationary and down going light will be traveling at almost twice the speed of light. In reality such a local observer see both up going light and down going light traveling at exactly the normal speed of light. The river model does not seem very good to me or I am missing the point somewhere.

The river model is derived from Painleve coordinates, so it does look a little strange if you're used to thinking of everything in Schwarzschild coordinates. Consider that the Painleve observer, who is free-falling into the hole "from infinity" (so his inward velocity is always the "escape velocity") also sees ingoing and outgoing light traveling, relative to him, at the speed of light. If he is just a little bit above the horizon, and then adjusts for the speed of the river, then he will say that relative to the "river bed", the ingoing light *is* moving inward at almost twice the speed of light, and outgoing light *is* almost stationary, just barely crawling outward.

To see what this situation looks like from the viewpoint of the "hovering" observer, we take the free-falling observer's picture and boost it, outward, by the "escape velocity", which in this case (just outside the EH) is almost the speed of light. (Strictly speaking, this tells us what things look like in the instantaneous local inertial frame of the hovering observer, at the instant the free-falling observer passes him. But since SR is locally valid, we can deduce all the local physics as seen by the "hovering" observer from this.) What do we find? The ingoing and outgoing light are still moving at the speed of light, relative to the "hovering" observer; but now the ingoing light is strongly blueshifted and the outgoing light is strongly redshifted.

So it is true that, to the "hovering" observer, the light is *not* moving relative to the "river bed" the way the free-falling observer says it is. That's OK because the "river bed" is not physically real anyway; it's just a visualization tool. I suggested the river model because I thought it might help the OP to see how things could look perfectly "normal" to the free-falling observer even as he and the blinker cross the horizon, while still obeying the global requirement that light cannot escape from inside the horizon to outside. I did not mean to claim that the river model is helpful for *all* aspects of the physics of black holes, or that it captures all aspects of that physics in a "natural" way.

 

[Rock2shark]

So it is true that, to the "hovering" observer, the light is *not* moving relative to the "river bed" the way the free-falling observer says it is. That's OK because the "river bed" is not physically real anyway; it's just a visualization tool. I suggested the river model because I thought it might help the OP to see how things could look perfectly "normal" to the free-falling observer even as he and the blinker cross the horizon, while still obeying the global requirement that light cannot escape from inside the horizon to outside. I did not mean to claim that the river model is helpful for *all* aspects of the physics of black holes, or that it captures all aspects of that physics in a "natural" way.

In my mind any discussion about the nature of and physical properties present at a distant relativistic type of condition requires a specification of the reference point from which the observation is made?

If we are to analyse the physical circumstances and observations of the observer hovering above the event horizon of a black hole, is it not helpful to proceed in the following way:

Using identical rigid rods of equal length and identical accurate clocks we construct a 3 dimensional rectangular frame, starting from our own location in space and extending sufficiently to contain the whole of our galaxy. We maintain synchronisation of the clocks so that the frame serves as a physical realisation of the reference frame in which we are stationary. The reference frame is an extension of the SR of our own location in space and serves to provide a basis for measuring the motion of distant bodies relative to ourselves as primary observers.

When we place an observer just above the event horizon, the observer must be stationary with respect to the reference frame, otherwise the statement ‘hovering above the event horizon’ is ambiguous in its meaning?

 

[PeterDonis]

Using identical rigid rods of equal length and identical accurate clocks we construct a 3 dimensional rectangular frame, starting from our own location in space and extending sufficiently to contain the whole of our galaxy.

This construction, which is familiar from introductory texts on SR, works globally for flat spacetime, where there is no gravity; it does *not* work globally in the presence of gravity. In the presence of gravity, you can only do this construction *locally*--i.e., for a small patch of spacetime centered on some particular event.

We maintain synchronisation of the clocks so that the frame serves as a physical realisation of the reference frame in which we are stationary.

Again, you can only do this locally in the presence of gravity; clocks which start out synchronized at different spatial locations in the presence of gravity will not stay synchronized.

When we place an observer just above the event horizon, the observer must be stationary with respect to the reference frame, otherwise the statement ‘hovering above the event horizon’ is ambiguous in its meaning?

The statement "hovering above the event horizon" does not require the construction of a local inertial frame to be given an unambiguous meaning. It simply means staying at the same radial coordinate r; the radial coordinate is defined as the "reduced circumference" of a 2-sphere at that radius, i.e., the circumference of the 2-sphere at r is 2 pi r and its area is 4 pi r^2. In principle r could therefore be measured without ever having to use the construction of a local inertial frame.

Also note that a local inertial frame, constructed as above, will only stay "hovering" at a given radius above the hole for an instant. For that instant, the "hovering" observer is at rest relative to this frame, yes. But a bit later, that particular inertial frame will have fallen towards the hole; the "hovering" observer, who is firing rockets to stay at a constant radius for all time, will now be at rest relative to a *different* local inertial frame, which is momentarily at rest at the appropriate radius at that later instant.

 

[Rock2shark]

Thank you for your explanation.

Also note that a local inertial frame, constructed as above, will only stay "hovering" ...

I understand in principle that the physical reference frame that I described is instantly distorted and wrecked by the bending of spacetime caused by the presence of gravitatoinal masses in the region of the framework. What I wished to describe was a frame that is not real, only imaginary, one that, because it is imaginary, is also immune to the effects of the massive bodies and the resulting accelerations of actual bodies and spacetime within the region covered by this imaginary reference frame.

In my mind I can picture this reference grid and the frame it provides within which an observer ‘O’ at a distance from the black hole is stationary. This is an imaginary grid that it would seem would provide a reference tool by which it seems it should be possible to measure the net effect relative to the observer at ‘O’ of gravitating bodies relative to the flat spacetime that would exist if those bodies and all gravitation were absent from the region. This would be done througth the eyes of a second observer placed at a point ‘A’ which is stationary relative to the frame of 'O' and which is also located corresponding close to or actually on the event horizon whilst fixed in relation to the imaginary 'special' frame may therefore (theoretically) at leisure take measurements of, say, the speed and other properties of bodies that are in real spacetime and which are therefore free falling towards the black hole and approaching and crossing the event horizon.

Does a flat spacetime of the kind described by the imaginary gridded reference frame in which 'O' and 'A' are stationary not provide a suitable kind of absolute reference?

Would the measurements taken by the observer at ‘A’ of the properties of bodies in real ‘actual’ spacetime not reflect the predictions of GR and the field equations?

I am intrigued by this question, and am endeavouring to gain as much understanding of GR and the tensor mathematics of GR and the Schwarzschild phenomena as I possibly can.

 

[PeterDonis]

I understand in principle that the physical reference frame that I described is instantly distorted and wrecked by the bending of spacetime caused by the presence of gravitatoinal masses in the region of the framework. What I wished to describe was a frame that is not real, only imaginary, one that, because it is imaginary, is also immune to the effects of the massive bodies and the resulting accelerations of actual bodies and spacetime within the region covered by this imaginary reference frame.

There is no such thing. The reason such an "imaginary" frame works in SR, in flat spacetime, is that we can pick out geometric objects in the flat spacetime that correspond to the imaginary reference frame. In curved spacetime, we can't; there are no such geometric objects, not even imaginary ones. In other words, in curved spacetime, even imaginary rods are bent and distorted by gravity, and even imaginary clocks run at different rates at different points.

Another way to put this is, in SR, in flat spacetime, we can use the math of the theory to tell us how imaginary rods and clocks behave. In curved spacetime, we can't; the math of the theory does not describe *any* objects that are not affected by gravity. So even if we were to postulate imaginary rods and clocks that were somehow unaffected by gravity, we have no way of making any statements at all about their behavior, so it's the same as if such objects did not exist.

In my mind I can picture this reference grid and the frame it provides within which an observer ‘O’ at a distance from the black hole is stationary. This imaginary grid appears to provide a reference tool by which it seems it shouild be possible to measure the net effect relative to the observer at ‘O’ of gravitating bodies relative to the flat spacetime that would exist if those bodies and all gravitation were absent from the region.

You may think you can imagine this, but if you try to work out a consistent set of predictions from it, you will find that that requires extra assumptions that are not always valid. For example:

A second observer placed at a point ‘A’ which is close to or actually on the event horizon, and who is at rest relative to the frame of the observer at point ‘O’ (and who is therefore also imaginary) may (theoretically) at leisure take measurements of, say, the speed and other properties of bodies free falling in real spacetime into the black hole and approaching and crossing the event horizon.

It's not just that such an observer is imaginary; an observer who "hovers" at or inside the event horizon would have to travel at or faster than the speed of light. But that is inconsistent with the way you wanted to set up the imaginary reference frame; setting up that frame requires that observers at rest in the frame travel slower than light.

Does a flat spacetime of the kind described by the imaginary gridded reference frame in which 'O' and 'A' are stationary not provide a suitable kind of absolute reference?

No. See above.

Would the measurements taken by the observer at ‘A’ of the properties of bodies in real ‘actual’ spacetime not reflect the predictions of GR and the field equations?

There can't be any such observer at or inside the horizon. Outside the horizon, yes, you can have an observer that "hovers" at a constant radius, and that observer's measurements will match the predictions of GR. But of course we do not need to set up any imaginary frame to derive those predictions. We can derive them, if we really want to, without using any frame of reference, any coordinates, at all; we can express everything entirely in terms of invariants, things that are independent of all coordinates.

Now, having said all that, I should note that, for the special case of a stationary black hole, there actually *is* a model that sort of has an "imaginary background reference frame that is static". It's called the "river model", and you can read about it here:

http://arxiv.org/abs/gr-qc/0411060

The key thing that allows the "background" (or "river bed") to work in this model is that it does *not* obey the laws of relativity--for example, things can move relative to the "river bed" faster than light. So it does *not* qualify as the sort of imaginary reference frame you were describing. But it does provide a way of visualizing what's going on in the spacetime around a black hole that may be easier to work with for that special case.

 

[Spin-Analyser]

The last time I didn't understand something the thread got locked so I'm going to have to be careful. I can't understand it until I know what would happen if an object approaches the event horizon and an object that had previously headed towards it. Please just tell me what happens.

1). The first object appears to cross the event horizon from the perspective of the second object but doesn't actually cross it until the second object reaches the event horizon.

2.) The first object crosses the event horizon from the perspective of the second object before the second object reaches the event horizon.

3). The first object doesn't reach the event horizon until the second object also reaches the event horizon.

If it's 1 then there's two horizons and if the second object were to move away before reaching the event horizon it would see the first object move backwards so that it's outside the horizon from a distance.

2 seems to be the one that fits in with the river model and the view that nothing special would happen in you crossed the event horizon of a super massive black hole. Then what happens if they're attached to each other with an extremely strong rope and the second object moves away from the black hole and when the first object is no longer inside the event horizon from the second objects perspective the rope goes taut and the second object pulls the first object away?

If it's 3 then everything that ever happens happens outside of event horizons and there is no interior.

 

[PeterDonis]

Please just tell me what happens.

2 is the correct answer (with some clarifications--see below).

Then what happens if they're attached to each other with an extremely strong rope and the second object moves away from the black hole and when the first object is no longer inside the event horizon from the second objects perspective the rope goes taut and the second object pulls the first object away?

What you've just described, as it stands, is impossible. If the second object accelerates away from the hole hard enough to keep from falling in, before it reaches the horizon but after the first object has crossed the horizon, there is no way to pull the first object back; the rope will break. The reason the rope will break can be phrased in two ways, which are consistent but which focus on somewhat different aspects of the situation:

A) The rope breaks because the lower end of it, the one attached to the first object, would have to travel faster than the speed of light to keep up with the upper end. Since it can't, the two ends move apart and the rope breaks.

B) The rope breaks because relativity imposes a limit on the tensile strength of materials (basically, the limit is that the speed of sound in the material can't exceed the speed of light). In order to keep from crossing the horizon, the second object must accelerate hard enough that the force it exerts on the rope will exceed the limit on the rope's tensile strength. So the rope breaks.

 

[Spin-Analyser]

And what's to stop information about the first object escaping from inside the event horizon?

 

[Nugatory]

And what's to stop information about the first object escaping from inside the event horizon?

Through what pathway? If you're thinking that a signal can be sent by tugging on the rope, or sending electrical impulses along the rope, or whatever... No matter how soon after the object crosses the horizon, and no matter how fast (but below the speed of light, of course) the signal travels, it will be stopped by the broken end of the rope somewhere inside the event horizon.

 

[PeterDonis]

And what's to stop information about the first object escaping from inside the event horizon?

The same thing that stops the first object itself from escaping from inside the horizon: information can't travel faster than light.

 

[PeterDonis]

No matter how soon after the object crosses the horizon, and no matter how fast (but below the speed of light, of course) the signal travels, it will be stopped by the broken end of the rope somewhere inside the event horizon.

It's even stronger than that: no signal emitted at a given radius r < 2M (i.e., inside the horizon) can reach a "receiver" at any radius greater than, or even equal to, the radius at which it was emitted. For example, if the first observer tries to send a signal up the rope (by shaking it, for example), the rope will fall (decrease in radius) *faster* than the signal moves up the rope. So when the signal reaches the broken end of the rope, that end will be at a *smaller* radius than the first observer was when he emitted the signal.

In the "river model", this is easy to visualize: the "river" inside the horizon flows inward faster than light, so any signal, even light, is carried inward faster than it can move outward against the river--its net motion is inward.

 

[Spin-Analyser]

You're saying that the second object sees the first object crossing the event horizon before the second object reaches the event horizon themselves, and no information can escape in an outwards ditrection from anywhere inside the horizon. The only way those two statements can be logically reconciled is if the image of the first object is frozon after it has crossed the event horizon from the second objects perspective?

 

[PeterDonis]

You're saying that the second object sees the first object crossing the event horizon before the second object reaches the event horizon themselves

This description is somewhat ambiguous. Let me give a more precise description of what happens.

The second object will "see" (receive light rays from) the first object crossing the horizon, at exactly the instant when the second object crosses the horizon. That is because the horizon is a lightlike surface: light rays emitted at the horizon stay at the horizon. (Strictly speaking, *outgoing* light rays--light rays emitted radially outward--stay at the horizon; I'm assuming that's the only kind of light rays we're talking about here.) So the light rays emitted by the first object at the instant when it crosses the horizon, stay at the horizon, and are met there by the second object at the instant when *it* crosses the horizon.

When the second object meets, at the horizon, the light rays from the first object crossing the horizon, that makes it clear that the first object must have crossed the horizon already; otherwise the light rays from its doing so wouldn't be there. So the first object crosses the horizon "from the second object's perspective" before the second object does. But the second object can't be absolutely sure of that until it reaches the horizon itself and sees the light rays left behind there by the first object. As long as the second object is outside the horizon, it can't "see" any light from the first object that was emitted at or inside the horizon.

The only way those two statements can be logically reconciled is if the image of the first object is frozen after it has crossed the event horizon from the second objects perspective?

Yes, one could use the word "frozen" to describe what happens to the "image" of the first object, if by "image" you mean simply "light rays emitted". Light rays emitted at the horizon stay at the horizon, so if that counts as "frozen", then yes, the image of the first object is frozen. Do you think this is a problem? If so, why? Or are you using the word "frozen" to mean something else? If so, what?

 

[Spin-Analyser]

So how does that fit in with the idea that nothing special happens from the perspective of a faller crossing the event horizon of a super massive black hole when you're saying they would see the light of everything that had crossed the event horizon pile up in front of them as they approach the event horizon to all be in the same place at the same time in the instant that the faller reaches the horizon, presumably in a blinding flash?

 

[PeterDonis]

So how does that fit in with the idea that nothing special happens from the perspective of a faller crossing the event horizon of a super massive black hole when you're saying they would see the light of everything that had crossed the event horizon pile up in front of them as they approach the event horizon to all be in the same place at the same time in the instant that the faller reaches the horizon, presumably in a blinding flash?

The idea that "nothing special happens from the perspective" of the infaller is a local statement; he can't tell that he's at the event horizon by making local measurements.

Receiving light signals at the horizon from all the other objects that have previously crossed it is not a local measurement. It's caused by the global properties of the spacetime, in particular the fact that there is enough curvature to make an event horizon. Similar remarks apply to other phenomena the infaller might observe, for example that light coming into him from sources far away from the hole will be heavily blueshifted.

 

[Spin-Analyser]

Either "they would see the light of everything that had crossed the event horizon pile up in front of them as they approach the event horizon to all be in the same place at the same time in the instant that the faller reaches the horizon, presumably in a blinding flash" is a local measurement as well or the second object is receiving information from inside the event horizon if they can tell if a previously falling object has reached the horizon before reaching it themselves.

 

[PeterDonis]

Either "they would see the light of everything that had crossed the event horizon pile up in front of them as they approach the event horizon to all be in the same place at the same time in the instant that the faller reaches the horizon, presumably in a blinding flash" is a local measurement as well or the second object is receiving information from inside the event horizon if they can tell if a previously falling object has reached the horizon before reaching it themselves.

I'm not sure where you're getting all this from; you seem to be either reading things into my post that I'm not saying, or bringing in other assumptions that are incorrect. Let me try to clarify some more.

Light emitted *at* the horizon stays at the horizon; nothing comes from inside the horizon to the horizon, and nothing goes from the horizon to outside the horizon. The second object can tell that the first object reached the horizon before him because the light from the first object is there, *at* the horizon; he doesn't need any information from inside. What the second object *can't* tell, just from the light at the horizon, is how *long* before him the first object crossed. (He could in principle tell that by extrapolating from observations he made of the first object while that object was still outside the horizon, but he can't tell anything from the light he sees at the horizon by itself.)

What I mean by "not a local measurement" is "not local in spacetime". The light that "piles up" at the horizon from objects that crossed it previously is not "local" because the horizon is not a local part of spacetime; it has global extent. The light that is "piled up" there would have to have come from objects that crossed the horizon over a long period of time. "Local" would mean you would only have light from objects that crossed over a very short period of time, right before the observer that is detecting the light, and that would be a very limited amount of light and would not be distinguishable from light emitted by nearby objects in free space, far from any gravitating bodies, so just by local light the infalling observer could not tell he was at the horizon.

 

[Spin-Analyser]

If light at the horizon stays at the horizon then they do see the light pile up in front of them locally as they approach the event horizon, and what if the rope that's attaching them were to go taut after the second object has seen the first object reaching the event horizon and has then moved away to a point in spacetime where the first object hasn't reached the horizon yet? The second object would be able to pull the first object away after witnessing it crossing the event horizon.

 

[pervect]

I'm not sure why the other thread was locked, unless you're banning questions? I'll ask it in as clear a way as possible.


When an observer approaches an event horizon to one plank length away one of two things must happen:

1). Any observers previously falling towards the black hole would be right along side you.

2). There is distance between you and the light from previous in-falling observers when you're right on the horizon. That would mean you would have to be seeing light from inside the horizon, although it's light that hasn't reached the horizon yet, which is paradoxical because you can't tell if they crossed. How can you be hovering the same distance away from the horizon as a previous observer and have space between you?

Please define the parameters of the universe in which that's supposed to make sense.

I"m afraid that a) I don't follow your logic and b) this is actually a question about quantum gravity, rather than a question about general relativity.

If you can rephrase your question in terms of millimeers rather than plank lengths, and provide the supporting reasoning behind your conclusions (which seem to come out of thin air), I could take a shot at it. Otherwise, I'd have to recommend reposting it to a forum that discusses quantum gravity. Since there are many different theories of quantum gravity, you'll additionally need to specify which one you want to use to have any chance of getting an answer - along with clarifying your logic. And once you've done all this, there may or may not be an answer out there, as the field is still being developed.

Not all quantum gravity theories are going to have any sort of "minimum length" scale. Many will have the structure of space-time become a "quantum foam", in which length simply becomes rather ill-defined if you look at it too closely. See for instance
http://en.wikipedia.org/wiki/Quantum_foam. I'd guess some sort of lattice theory (if it exists) would be your best bet.

About all I know about lattice theories is that keeping the Poincare symmetry becomes a problem.

 

[PeterDonis]

If light at the horizon stays at the horizon then they do see the light pile up in front of them locally as they approach the event horizon

No, they don't. Remember it's light we're talking about; you don't see it until you reach it. The infalling observer doesn't see any of the light at the horizon until he is *at* the horizon; before then he sees none of it. So there is no "piling up" of light the way you're describing it.

Also, remember, once again, that the only reason there would be a lot of light "piled up" at the horizon for the second observer to see when he reaches it would be that a *lot* of objects have previously crossed the horizon, over a long period of time. Again, that is not a "local" phenomenon. In your original scenario, the only two things crossing the horizon were the first observer and the second observer. In *that* scenario, there would not be any light "piled up" at the horizon: when the second observer sees the light that the first observer emitted at the instant he crossed the horizon, the image will look just like any other image of the first object. The second observer will not be able to tell, just from the image, that the first observer was at the horizon when he emitted it (or indeed that the second observer, himself, is at the horizon when he receives it).

and what if the rope that's attaching them were to go taut after the second object has seen the first object reaching the event horizon

If the second object has seen the first object reaching the horizon, then the second object has reached the horizon himself.

and has then moved away to a point in spacetime where the first object hasn't reached the horizon yet?

Impossible, for two reasons:

(1) The second object has already reached the horizon (see above), so he can't go back outside it.

(2) Moving to "a point in spacetime where the first object hasn't reached the horizon yet" would require moving backwards in time. Any such point in spacetime is in the *past* of the second observer, so he can't "move to" it.

The second object would be able to pull the first object away after witnessing it crossing the event horizon.

No, he wouldn't. See above.

A general comment: I suspect that, without realizing it, you are making hidden assumptions about space and time and how they work that are, in fact, false, though they are intuitively appealing. It might help if, instead of just stating conclusions you are drawing about the scenario we are discussing, you would go into more detail about the reasoning that is leading you to those conclusions.

 

[Spin-Analyser]

At the very least they would create an optic boom from there own light as they break the light barrier. In the case of a small super massive black hole near the end of its life with lots of light from all the matter that had ever crossed the event horizon anywhere near that side of the black hole piling up in front of the event horizon, a falling object wouldn't see the light waves building up but would see a blinding flash when reaching the event horizon and then everything would be pitch black because no light from further in can reach them. That contradicts the idea that nothing special happens locally for a falling object when crossing the event horizon.

 

[PeterDonis]

At the very least they would create an optic boom from there own light as they break the light barrier.

They can't "break the light barrier"; nothing can go faster than light. It's true that the correct formulation of that rule is more complicated in curved spacetime, but none of the complications make an "optic boom" possible.

(It's also true that in a material medium, something like an "optic boom" is possible, when objects travel faster than the speed of light in the medium, which can be slower than the speed of light in vacuum. This is called Cerenkov radiation. But here we're talking about vacuum and the speed of light in vacuum, so none of that applies.)

In the case of a small super massive black hole near the end of its life with lots of light from all the matter that had ever crossed the event horizon anywhere near that side of the black hole piling up in front of the event horizon, a falling object wouldn't see the light waves building up but would see a blinding flash when reaching the event horizon

Yes, this is correct, but it is not a "local" phenomenon. See below.

and then everything would be pitch black because no light from further in can reach them.

But light from further out still can, so it wouldn't be pitch black. It's true that the light coming in would be distorted, but again, that's not a "local" phenomenon, because the light has to come from distant locations to be distorted. Light from locations close to the infalling observer is not distorted, and the infalling observer can't tell from it that he is at or inside the horizon.

That contradicts the idea that nothing special happens locally for a falling object when crossing the event horizon.

No, it doesn't. I already explained why: all the light in the "blinding flash" was built up at the horizon over a long period of time. That is not a "local" phenomenon; it requires the horizon and the hole to exist for a long period of time. "Local" means local in space *and* time. The same goes for the other items above, such as light coming in from distant locations being distorted--they're not local because they require a large extent of space, or a long period of time, or both. Your repetition of incorrect statements after they've already been corrected is part of what got your last thread locked.

 

[Spin-Analyser]

If I get an answer that doesn't make sense to me then I'm going to have to go over it again, sorry. So you agree that the fallers view of the interior is dark and all the light coming to them after passing the event horizon is coming from outside, and the second object would see the first object and all other previously falling objects disappear after reaching the event horizon?

If the light builds up in front of a falling object until it reaches the horizon then how is the flash not a local phenomenon? If not and light always moves away normally from the falling object locally, even when and after crossing the event horizon then the light from previously falling objects is crossing the event horizon from the falling objects perspective before the falling object reaches the event horizon. You keep switching between the two. Either there is a local optic boom or information is escaping from inside the horizon. It can't be both, and it definitely can't be neither.

 

[DrGreg]

Either there is a local optic boom or information is escaping from inside the horizon. It can't be both, and it definitely can't be neither.

Actually it is neither.

Imagine you are traveling down a straight road, and you are following a convoy of trucks in front of you. All you can see is the back of the last truck. Light from the other trucks never reaches you because it hits another truck. If the last truck were semi-transparent, you'd see light from the last truck and the one in front of it both hitting your eyes at the same time, although the light from the front truck would be delayed more than the light from the back truck. With standard opaque trucks, you just see the back truck.

It's no different if the convoy of trucks were falling into a black hole. At the exact moment you reach the event horizon, light from the last truck, emitted earlier when it reached the event horizon, will hit your eye. You won't see light from the other trucks, because that light would already have been absorbed by the front of another truck.

So you won't get a huge flash of light as you cross the event horizon. You will just see the most recent thing to have crossed that part of the event horizon. Light from anything else that crossed the horizon earlier would have been absorbed by something else crossing the horizon. And the thing you see as you cross the horizon (e.g the back of the last truck) is the same thing you would have already been seeing before you crossed the horizon and will continue to see after crossing the horizon.

Light from objects already inside the horizon never reaches the horizon; light at the horizon is only from the most recent object to have crossed it, emitted when it crossed it.

 

[PeterDonis]

If I get an answer that doesn't make sense to me then I'm going to have to go over it again, sorry.

I have no problem with this per se, but many of the "answers" that don't make sense to you are not answers I have given you; they are things you have added in yourself. For example:

So you agree that the fallers view of the interior is dark and all the light coming to them after passing the event horizon is coming from outside, and the second object would see the first object and all other previously falling objects disappear after reaching the event horizon?

No, I do not agree, and if you are deducing any of this from what I've said, then you are deducing incorrectly.

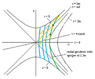
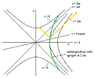
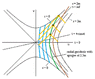
Here is what you can correctly deduce from what I have said: any light reaching an infaller after he has crossed the horizon and is inside it, must have been *emitted* from a larger radius than the infaller is at when he *receives* it. So, for example, if the second observer receives, inside the horizon, a light signal emitted by the first observer, then the first observer must have *emitted* that signal when he was at a larger radius than the second observer is at when he *receives* it. This is perfectly possible, so the second observer will *not* see the first observer disappear once he has passed inside the horizon.

This means that even outgoing light, inside the horizon, moves inward--but it moves inward more slowly than the infallers do (the first and second observers), so an infaller can "catch up" to a light signal that was emitted by another infaller who crossed the horizon before him and remains below him as he continues to fall.

Another example of you adding in things I have not said:

If the light builds up in front of a falling object until it reaches the horizon then how is the flash not a local phenomenon?

Light does *not* "build up in front of a falling object". I have not only not said this, I have explicitly *denied* it. I have already explained, twice, how the flash is a "local phenomenon". Please re-read my explanation (plus what I've added below about the precise meaning of "local"), and then if you still have questions, by all means ask them; but ask them about what I actually wrote, not about things I have not written and have specifically said already that I have not written. If you simply can't let go of this picture you have of light "building up in front of an falling object", then you're going to have to explain, in detail, how you are coming up with that picture. Just re-asserting it won't do.

If not and light always moves away normally from the falling object locally

It's very important to understand precisely what "locally" means. I haven't given a precise statement yet in this thread, so I'll do so now. Strictly and precisely speaking, "locally" means "in the local inertial frame of a specific observer, centered on a specific event on that observer's worldline".

I don't know how familiar you are with the terms I just used, so let me expand on the precise definition I just gave. An "event" is a point in spacetime--a particular point in space at a particular instant of time. Physically, we identify events by what happens at them; for example, "the second observer crosses the horizon" is an event. If we want to be more precise, we can locate events in spacetime by the intersection of two curves: for example, the event I just gave could also be described as "the intersection of the second observer's worldline with the horizon". Both the worldline and the horizon are curves in spacetime, and their intersection is a point, so that is sufficient to pin down a specific event.

A local inertial frame is a way of making a small patch of an arbitrary curved spacetime look like a small patch of flat Minkowski spacetime--the spacetime of Special Relativity. It works like this: first we pick a particular event on a particular observer's worldline, such as the one described above--the second observer crosses the horizon. Then we restrict ourselves to a small enough range in space and time around that event that the effects of spacetime curvature--tidal gravity--can be ignored. Then we set up standard inertial coordinates, the ones we use in flat Minkowski spacetime, with the event we picked as the origin, and with the observer's worldline as the time or "t" axis. We can in principle orient the spatial axes any way we like; here the easiest thing is to orient our "x" axis radially; i.e., positive "x" points radially outward, and the line x = 0 is the second observer's worldline. However, bear in mind that the surfaces of simultaneity--the surfaces of constant time--in this local frame are those of the infalling observer, so they are really small pieces of surfaces of constant Painleve time; they are *not* surfaces of constant Schwarzschild time (which would be the surfaces of constant time for observers "hovering" above the horizon).

Now, within this local inertial frame, physics works the same as it does in SR; we can basically ignore gravity (except that of course being "at rest" in this local frame means free-falling into the hole). So suppose that the first observer was just a little in front of us when he crossed the horizon. Then, since the second observer is at x = 0, the first observer will be at some slightly negative value of x; say x = -1, where we scale the x coordinate appropriately so 1 unit is a small enough distance. Then, what does the horizon look like in this local frame? Well, it is an outgoing lightlike surface, and it has to pass through the origin (since that's the event where the second observer crosses it), so it will be the line x = t (sloping up and to the right at 45 degrees--we are using units where the speed of light is 1).

So in this local frame, the first observer will cross the horizon at x = -1, t = -1. If he emits a light signal radially outward (towards us) at that event, it will have the same worldline as the horizon, so it will reach the second observer at the origin--x = 0, t = 0. The light moves away from the first observer at speed 1, in this local frame, just as in flat spacetime; and it moves towards the second observer at the same speed, just as in flat spacetime. Everything works just the same as if both were in flat spacetime--within this small local frame.

However, remember what I said above about the limits in space and time of this local frame; it has to be small enough that tidal gravity can be ignored. Suppose there were some other observer that crossed the horizon a long while before the first observer--long enough that tidal gravity can no longer be ignored. Then we could not fit that observer's worldline into the local frame we constructed above, and we could not use that frame to predict what would happen to light signals from it. We would have to use our global knowledge of the spacetime, such as the fact that the horizon is an outgoing lightlike surface, globally, to tell us that light emitted by that previous observer, at the instant he crossed the horizon, would be received by the first observer at the instant when *he* crossed the horizon.

It can't be both, and it definitely can't be neither.

I agree with DrGreg's post on this. In particular, he brings up a good point that I had not considered: if we have multiple objects crossing the horizon, each one absorbs the light from the previous one.

 

[Spin-Analyser]

Hold on, let me just get this straight. You're both saying that light doesn't build up at the event horizon because it catches a lift from the matter that falls in behind it and move quicker than it would do otherwise preventing a flash of light when an object crosses an event horizon?


Either,

when an object is falling towards a black hole the light from all previously falling observers is building up between them and the event horizon. Light from the falling object always leaves them locally at the full speed of light and slows as it approaches the event horizon in front of them, creating a build up of light waves at the front of the falling object in the same way that an object approaching the sound barrier experiences a build up of sound waves before creating a sonic boom. As the object approaches the event horizon the extended area where special relativity still applies locally (as in the area where light is still able to move away from the falling object at the speed of light up to a certain distance away) shrinks to nothing at the event horizon, because the falling object is passing the point where an object even one mm in front of them is falling away from them faster than light. Once the falling object is passed the event horizon any object further in is falling away from it faster than light so no light from previously falling objects can ever reach an object that has crossed the event horizon because the rate that objects in front of it accelerate away only increases once inside the event horizon, and no light from outside would be able to reach you because you'd be outaccelerating it, so it would be pitch black,

or,

you can't overtake your own light and there is always an extended area where special relativity still applies. If this is the case then a falling object can see a previously falling object crossing the event horizon before reaching it themselves.

 

[yuiop]

Hold on, let me just get this straight. You're both saying that light doesn't build up at the event horizon because it catches a lift from the matter that falls in behind it and move quicker than it would do otherwise preventing a flash of light when an object crosses an event horizon?

Neither of them are saying that there is no build up of light "because it catches a lift from the matter that falls in behind it". The infalling observer does not see an unusual flash of light at the event horizon, because he always sees light from the previously infalling observers, before, during and after passing the event horizon. Please see the first attached sketch titled "past" in Kruskal-Szekeres coordinates. The green curve is the path of the primary falling observer. The blue curves are the paths of previously infalling observers. The diagonal orange lines are light rays from the infalling observers. At event (a) outside the event horizon, the observer sees light from all 3 previously infalling observers. At event (b) the primary observer is at the event horizon and sees light from all 3 previously infalling observers that was emitted at the time they passed the event horizon. At event (c) the primary observer is inside the black hole and nearly at the singularity and he still sees light from all 3 previously infalling observers from when they were also inside the event horizon. Note that the primary observer never sees light from observers inside the event horizon, while he is outside the event horizon. Especially note that he never sees an unusual flash of light as he arrives at the event horizon. This is nothing to do with the light from previously infalling observers intersecting the light from other infalling observers. There still would be no unusual flash of light at the event horizon, if all previous infalling observers were transparent, or if they were slightly offset from the same radial path so that they are not hiding behind each other.

.. when an object is falling towards a black hole the light from all previously falling observers is building up between them and the event horizon.

Not true. Again see the first attached drawing.

.. Once the falling object is passed the event horizon any object further in is falling away from it faster than light so no light from previously falling objects can ever reach an object that has crossed the event horizon because the rate that objects in front of it accelerate away only increases once inside the event horizon, and no light from outside would be able to reach you because you'd be outaccelerating it, so it would be pitch black,

Also not true. In the attached diagram the observer at event (c) inside the event horizon still sees light from previously infalling observers, so it is not pitch black.

or,

you can't overtake your own light and there is always an extended area where special relativity still applies. If this is the case then a falling object can see a previously falling object crossing the event horizon before reaching it themselves.

Also not true. The falling observer only sees previously infalling observers crossing the event horizon, when he himself is also crossing the event horizon. This is event (b) on the attached sketch.

The second attached sketch called "future" demonstrates that light (the diagonal orange lines) from the falling observer (green curved path) does not "pile up" at the event horizon. The inwardly directed light ray goes straight through the event horizon. You can also note that once light is emitted from the infalling observer, that the infalling observer never catches up with the light because his path never again intersects with the light paths.

Just for reference, the diagonal black line going from bottom left to top right labelled r=2m is the event horizon and the curve labelled r=0 near the top is the singularity of the black hole.

 

[Spin-Analyser]

I follow you up to (c). If a falling object is just a mm away from the event horizon then a falling object just inside the horizon is moving away faster than light relative to the more distant faller. That difference in relative velocity between objects depending on how close they are to the singularity only increases inside the horizon, so a falling object wouldn't be able to catch any previously falling light and no light from the outside could catch the falling object once inside the event horizon, so it would definitely be black.

Forget the light from previously falling objects. When approaching the event horizon the light emitted towards the black hole from the falling object moves away from them at the speed of light to start with, but slowing as it nears the event horizon. As the gap between the falling object and the event horizon decreases, the length of the valid frame of reference where light is moving away from the falling object at c decreases as well, creating an optic boom in the same way a planes own sound waves create a sonic boom.

If on the other hand there's always a valid frame of reference where light is moving away from the falling object at c then there must be a point close to the horizon where a falling object can tell whether or not previously falling objects have reached the event horizon yet.

 

[PeterDonis]

Hold on, let me just get this straight. You're both saying that light doesn't build up at the event horizon because it catches a lift from the matter that falls in behind it and move quicker than it would do otherwise preventing a flash of light when an object crosses an event horizon?

I'm not sure I understand what you're trying to convey here, but I think the answer is no.

when an object is falling towards a black hole the light from all previously falling observers is building up between them and the event horizon.

Why do you think this? Once again, if you actually want to get the whole scenario here figured out, you're going to have to do more than just state this; you're going to have to explain, in detail, how you are arriving at this picture of what's happening.

One clarification, just to be sure it's clear: outgoing light only remains at the horizon if it is emitted *exactly* at the horizon. If it's emitted just a little bit outside the horizon, it moves outward--just not very much at first, though it still moves outward faster than a timelike object that is moving outward, like a rocket that has made a huge fuel "burn" to keep from falling below the horizon. If it's emitted just a little bit inside the horizon, it moves inward--just slower than timelike objects. So unless outgoing light is emitted exactly *at* the horizon, it doesn't "build up" in the same place.

Also, from the viewpoint of the infalling observer, the horizon is not "staying in the same place"--it is moving outward at the speed of light. (That's why light emitted outward at the horizon "stays" there.) So an infalling observer does not see light "build up" at the horizon; to him, the horizon is just a surface of light that moves outward past him.

Light from the falling object always leaves them locally at the full speed of light and slows as it approaches the event horizon in front of them

Remember we are talking about *outgoing* light here. Outgoing light emitted from a falling object outside the horizon moves outward; it does not move towards the horizon. Light emitted in other directions does not behave the same way. In particular, *ingoing* light does *not* stay at the horizon; it moves inward, faster than anything else that's moving inward. So ingoing light certainly does not "build up" anywhere; it races ahead of everything else that's falling in.

I won't comment further on this portion of your post because I think you are working from mistaken premises. I would suggest re-thinking your picture of things in the light of what I've said above, and in particular being careful to distinguish ingoing from outgoing light.

you can't overtake your own light

Correct.

and there is always an extended area where special relativity still applies

No, there is not an "extended area" where SR applies, in any curved spacetime. You can only apply SR within the confines of a local inertial frame, as I described in a previous post.

If this is the case then a falling object can see a previously falling object crossing the event horizon before reaching it themselves.

No, they can't. Once again, if you keep on asserting this without explaining, in detail, how you are arriving at this conclusion, we aren't going to get anywhere.

 

[PeterDonis]

If a falling object is just a mm away from the event horizon then a falling object just inside the horizon is moving away faster than light relative to the more distant faller.

No, it isn't. Why do you think it is?

One could say, perhaps, that an object freely falling just inside the horizon is moving faster than light relative to a *hovering* observer just outside the horizon; but that requires putting a particular interpretation on the behavior of the coordinates there. Such an interpretation is not required, and doesn't help you in making any physical predictions anyway. In any case, in a curved spacetime, there is no unique way of defining the relative velocity of objects except within the confines of a local inertial frame. If you do that for two objects both falling into the hole, one just inside the horizon and one just outside it, and you make sure that the hole is large enough compared to the distance between them that tidal gravity is negligible, then the two objects will have a relative velocity less than that of light, as evaluated within that local inertial frame. (In fact, you can make their relative velocity as small as you like by making the hole large enough.)

That difference in relative velocity between objects depending on how close they are to the singularity only increases inside the horizon

This effect is due to tidal gravity, so it can only be seen outside the confines of a local inertial frame. One of the consequences of that is that the allowed size of a local inertial frame gets smaller and smaller as you approach the singularity, because tidal gravity gets larger and larger.

, so a falling object wouldn't be able to catch any previously falling light

If by "falling light" you mean "ingoing light emitted earlier", then yes, this is true; ingoing light always falls faster than anything else.

and no light from the outside could catch the falling object once inside the event horizon,

Wrong. I have already explained why this isn't true, and it looks like yuiop has too. Since ingoing light falls faster than anything else, it can catch an infalling object.

When approaching the event horizon the light emitted towards the black hole from the falling object moves away from them at the speed of light to start with

Correct.

, but slowing as it nears the event horizon.

Wrong. Ingoing light does not slow down; it "speeds up", just as everything else does. Ingoing light always falls faster than anything else. I think you are again confusing ingoing with outgoing light; they don't behave the same in this scenario.

If on the other hand there's always a valid frame of reference where light is moving away from the falling object at c then there must be a point close to the horizon where a falling object can tell whether or not previously falling objects have reached the event horizon yet.

I don't understand how you are arriving at this conclusion. Are you talking about ingoing light here? If so, again, it behaves differently than outgoing light.

 

[Dale]

If a falling object is just a mm away from the event horizon then a falling object just inside the horizon is moving away faster than light relative to the more distant faller.

This is not correct. Suppose A is 1 mm away and B is 2 mm away from the EH of a supermassive black hole so that tidal effects are negligible, and suppose that they are free falling and at rest wrt each other. Then, because tidal effects are negligible they will still be at rest wrt each other as they cross and continue to free fall within the EH.

When approaching the event horizon the light emitted towards the black hole from the falling object moves away from them at the speed of light to start with, but slowing as it nears the event horizon. As the gap between the falling object and the event horizon decreases, the length of the valid frame of reference where light is moving away from the falling object at c decreases as well, creating an optic boom in the same way a planes own sound waves create a sonic boom.

None of this is correct. Can you explain why you think any of this?

If on the other hand there's always a valid frame of reference where light is moving away from the falling object at c then there must be a point close to the horizon where a falling object can tell whether or not previously falling objects have reached the event horizon yet.

You seem to forget that the event horizon is a null surface, meaning that in a coordinate independent sense it moves outwards at c. Since the EH moves at c, in order for information about whether or not an object has crossed the EH to reach an observer outside the EH it would have to go faster than c in a coordinate independent sense.

 

[yuiop]

I follow you up to (c). If a falling object is just a mm away from the event horizon then a falling object just inside the horizon is moving away faster than light relative to the more distant faller. That difference in relative velocity between objects depending on how close they are to the singularity only increases inside the horizon, so a falling object wouldn't be able to catch any previously falling light ...

The Kruskal-Szekeres diagram I posted in my last reply clearly shows that the falling observer does catch light from previously falling objects whilst inside the event horizon so your statement here is not correct. Did you even look at the diagrams or just fail to understand them?

... and no light from the outside could catch the falling object once inside the event horizon, so it would definitely be black.

I have attached an amended KS diagram "past2" that includes the light rays from an object that falls after the infalling observer and light rays from an object that remains outside the event horizon at r=3m. The infalling observer continues to receive light from both these objects (and previously infalling objects) outside and inside the event horizon. All objects that he can see while outside the event horizon are still visible when he is inside the event horizon. Your statement that "it would definitely be black" inside the event horizon is also not correct.

Forget the light from previously falling objects. When approaching the event horizon the light emitted towards the black hole from the falling object moves away from them at the speed of light to start with, but slowing as it nears the event horizon. As the gap between the falling object and the event horizon decreases, the length of the valid frame of reference where light is moving away from the falling object at c decreases as well, creating an optic boom in the same way a planes own sound waves create a sonic boom.

This "optic boom" effect you describe is clearly not present if you study the attached KS diagram. The KS chart is effectively the reference frame in which the infalling observer considers himself to be stationary. In this chart, the speed of light is always constant and not just locally so there is no slowing down of light near the vent horizon. In Schwarzschild coordinates, there is a sense in which the coordinate speed of light is slowing down but in the Schwarzschild chart, the infalling observer is also slowing down as he approaches the event horizon, so it is not clear that the falling observer is catching up with his own light. Everything near the event horizon appears to be "bunched up" near the event horizon in the Schwarzschild chart so that region is difficult to analyse in that chart. This apparent bunching up disappears in the KS chart that expands the event horizon region. This occurs partly because radial distances between events are measured to be much greater by the freefalling observer, relative to the measurements by the Schwarzschild observer in the region near the event horizon.

If on the other hand there's always a valid frame of reference where light is moving away from the falling object at c ...

That would be the KS chart in the diagrams I have attached ...

... then there must be a point close to the horizon where a falling object can tell whether or not previously falling objects have reached the event horizon yet.

... but again you have reached the wrong conclusion. There is no point outside the event horizon, where the falling observer sees light from events at or below the event horizon. Again, this should be very obvious from the KS diagrams I have attached.

 

[PeterDonis]

The KS chart is effectively the reference frame in which the infalling observer considers himself to be stationary.

No, it isn't. A "stationary" object in the KS chart is at a constant Kruskal X-coordinate, i.e., moving on a vertical line in your diagram; this is *not* the worldline of an infalling observer. (Your line "radial geodesic with apogee at r = 3m is one example of an "infalling observer", but it is not a vertical line.) A vertical line in the KS chart is not a geodesic.

In this chart, the speed of light is always constant

No, it isn't; at least not if by "speed of light in this chart" you mean the coordinate speed of light, dX/dT, where X and T are the Kruskal space and time coordinates (the horizontal and vertical axes in your diagram). The coordinate speed of light varies with position on the chart. This is because the "scale" of the chart (the relationship between coordinate differentials and actual physical proper times/proper distances) is not constant; it varies with position on the chart.

I think what you are trying to say is that the worldlines of light rays are always 45 degree lines: ingoing light rays move up and to the left at 45 degrees, and ougoing light rays move up and to the right at 45 degrees. This is true, and it is one of the things that makes this chart so useful. But the *speed* of light is *not* constant; the "rate at which light moves along the 45 degree lines" varies with position on the chart, because the scale of the chart varies as above.

there is no slowing down of light near the event horizon.

A better way to say this would be that light rays always move on 45 degree lines; their "direction" on the chart does not change. This also helps with better understanding the contrast with this...

In Schwarzschild coordinates, there is a sense in which the coordinate speed of light is slowing down

A better way of saying this is that the "direction" of light rays on the Schwarzschild chart changes with radius; they aren't always 45 degree lines.

but in the Schwarzschild chart, the infalling observer is also slowing down as he approaches the event horizon, so it is not clear that the falling observer is catching up with his own light.

This is true; the distortion of the Schwarzschild chart near the horizon makes it practically useless for answering questions of this sort. (You can still do the computation in Schwarzschild coordinates, in principle, as long as things remain outside the horizon, but it's very tedious compared to the computation in other charts.)

Everything near the event horizon appears to be "bunched up" near the event horizon in the Schwarzschild chart so that region is difficult to analyse in that chart. This apparent bunching up disappears in the KS chart that expands the event horizon region.

Yes.

This occurs partly because radial distances between events are measured to be much greater by the freefalling observer, relative to the measurements by the Schwarzschild observer in the region near the event horizon.

Is this true? I think it's the other way around, but it depends on how you interpret "radial distances" and how you interpret "distances measured by the freefalling observer". My interpretations are: pick two fixed radial r-coordinate values, r1 and r2. The radial distance measured between these two radial coordinates in Schwarzschild coordinates (i.e., along a line of constant Schwarzschild time) is *larger* than the distance measured between them in Painleve coordinates (i.e., a long a line of constant Painleve time). The latter is the most natural "distance" for the infalling observer (since Painleve time is the same as proper time for the infalling observer).

That would be the KS chart in the diagrams I have attached ...

If you interpret "moving away at c" as "moving along a 45 degree line", yes. But I would say that light "moves away from a falling object at c" only within the local inertial frame of the falling object, at the event where it emits the light. Beyond that you get into issues with trying to compare speeds at spatially distant locations in curved spacetime; the KS chart does not avoid those issues.

There is no point outside the event horizon, where the falling observer sees light from events at or below the event horizon. Again, this should be very obvious from the KS diagrams I have attached.

Definitely agree. Please note: I agree with the main substance of your post, since the key claims you are making about light rays and infalling observers are the same ones I've been making. But I think it's important not to confuse things by making statements about the KS chart that are either untrue or, at least, require interpretation that doesn't really help with the main topic of this thread.

 

[yuiop]

Please note: I agree with the main substance of your post, since the key claims you are making about light rays and infalling observers are the same ones I've been making. But I think it's important not to confuse things by making statements about the KS chart that are either untrue or, at least, require interpretation that doesn't really help with the main topic of this thread.

I agree with the fine points you mention, but as you mention, they do not alter the main substance of the points I was trying to make. However, I was guilty of being a bit sloppy. Thanks for the correction!

I think the statements I made in the last post would be more accurate if we considered a non inertial observer in a rocket accelerating towards the black hole, in such a way that the worldine of the rocket is a vertical line in the KS chart.

Either way, the points about the ingoing observer:

1) still seeing light from objects outside the event horizon when inside the event horizon.

2) still seeing light from previously infalling objects when inside the event horizon.

3) not seeing light from events at or inside the event horizon, while outside the event horizon.

remain valid.

 

[PeterDonis]

I think the statements I made in the last post would be more accurate if we considered a non inertial observer in a rocket accelerating towards the black hole, in such a way that the worldine of the rocket is a vertical line in the KS chart.

That would be a "stationary observer" in the KS chart, yes. The acceleration profile would be a weird one.

Either way, the points about the ingoing observer:

1) still seeing light from objects outside the event horizon when inside the event horizon.

2) still seeing light from previously infalling objects when inside the event horizon.

3) not seeing light from events at or inside the event horizon, while outside the event horizon.

remain valid.

Yes, definitely.