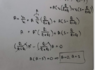jim hardy
Science Advisor
Homework Helper
Dearly Missed
- 9,864
- 4,896
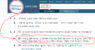
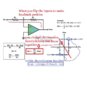
eq1 said:There is an algebra error. The fourth step from the bottom uses the substitution Vo=A(Vc) but the correct substitution is Vo=A(Vb), defined in your step 3. (Assuming I am reading your handwriting correctly that this. The subscripts are a bit small on my screen.)
here's the bottom five steps. Can you highlight your observation ?
eq1 said:The correct way to analyze the operating point is KCL at B. (b-c)/Ri = (o-b)/Rf substitute b=o/A and solve yielding o=A*c*Rf/(Rf+Ri-A*Ri) (thanks wolfram alpha!) As lim A->inf you get Vo=-c*Rf/Ri which is the correct answer.
I too solved for Vout using KVL for b, took limit as gain approaches infinity...
with infinite gain it's## Vin X (1 - \frac {Rfb + Rin}{Rin} ) ## which resolves to the same expression as yours
and only proves that Kirchoff's Laws agree.
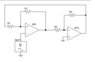
i strongly disagree. See post 35.eq1 said:This circuit can be perfectly stable.
Sitting on a cusp is not stable.
and it is a disservice to a beginner to infer otherwise.
This circuit does not develop any restoring forces to return it to equilibrium..
It does the opposite, develops a disrupting force that drives it away from equilibrium toward infinity
but it hits the power supply rail first.
It's a disservice to a beginner to claim otherwise.
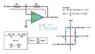
Vo=-c*Rf/Ri is NOT the mathematical operation that this circuit performs. To perform that one requires negative feedback.
What this circuit does mathematically is a logical computation with only two output states,
True and False,
represented by the maximum and minimum output values of Vout
"output state" = Vin + (Vout-Vin)X(Rin/(Rfb +Rin) > 0
where "output state" is a logical variable and the voltages (and R's) are real ones.
and (Vout-Vin)X(Rin/(Rfb +Rin) is just the voltage across Rin
Ahhhh, nostalgia.
I always modeled my circuits in Basic on my TI-99/4A,
and that Basic would assign to "output state" integer value,
either 0 (no bits set) for FALSE or -1 (all bits set for TRUE. .
That Basic was interesting , you could mix logicals and reals in an equation which was sometimes handy. But that's another story.
Anybody see algebra goofs or typos ? Please advise.
old jim
Attachments
Last edited: