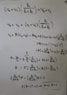GrahamN-UK
- 48
- 39
Abdullah Almosalami said:I could have gone wrong in the calculations, but I don't see it and no one has pointed out where,
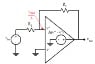
Actually, previous posters have pointed out where you went wrong but perhaps they were too subtle for you and their message has been lost in the formulas. So, here's the fundamental point you have missed: what you labelled as the "Voltage Rule of Ideal Op-Amps", Va = Vb, in the first diagram in post #1 IS ONLY VALID FOR NEGATIVE FEEDBACK AMPLIFIERS.
The feedback in a negative feedback amplifier acts to drive Va (in your circuit) to be equal to Vb. In a positive feedback amplifier the feedback acts to drive Va away from Vb. Hence Va is not equal to Vb in a positive feedback amplifier. The Voltage Rule is not valid for a positive feedback amplifier and you cannot use it to analyse a positive feedback amplifier.
The problem with your analysis in the second part of post #1 and in post #13 is that you have still included your Voltage Rule; the assumption that Va = Vb, in your analysis . That is why your analysis gives you the results you know to be wrong.
To analyse the positive feedback rule you'll need to use the formula gneill gave you in post #2: Vout = A(V+ - V-).
Note that putting the wrong formulas into a simulation will produce the wrong outputs, even if it does look very neat.
Abdullah Almosalami said:EE textbooks (like the two I've looked at) derive the equations for the standard inverting input case but always ignore the other way around.
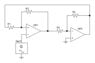
The standard equations are only valid for negative feedback circuits. There is no corresponding equation for a positive feedback amplifier because no corresponding positive feedback amplifier circuit exists. (You should however find an equation for a non-inverting negative feedback amplifier.)
Other posters have pointed out that an op-amp circuit with positive feedback gives you a comparator circuit with hysteresis, also known as a Schmitt trigger circuit. You may find an analysis of this circuit in your textbooks, or online.
Abdullah Almosalami said:What I was kind of hoping for was for someone to describe a more accurate model of an op amp that does account for all that was mentioned here.
You don't need a more accurate op amp model for this analysis. The introductory model is fine as long as you realize why your 'voltage rule of ideal op-amps' applies only to negative feedback circuits.
If you go back and re-read the thread, bearing in mind that your Voltage Rule is only valid for negative feedback amplifiers, you should find that the early posts do actually say this.