What is the acceleration and average speed of a car in circular motion?

[zebragiraffe]

A car initially traveling eastward turns north by traveling in a circular path at uniform speed as in the figure below. The length of the arc ABC is 265 m, and the car completes the turn in 32.0 s.

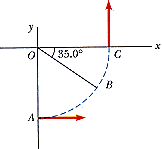
(a) What is the acceleration when the car is at B located at an angle of 35.0°? Express your answer in terms of the unit vectors i hat and j hat .

(b) Determine the car's average speed.


m/s

(c) Determine its average acceleration during the 32.0 s interval.
Equations

Ac=v^2/r

 

[BruceW]

You should really try the questions first, before asking for help. That's the rules of this forum..