What Is the Acceleration of a 77kg Skier Traveling at 45mph Downhill?

[benjaminwhite]

Homework Statement

Consider the downhill skier shown at the right (just a picture of a skier, no info given in picture). The skier has a mass of 77kg and is traveling at 45mph.

Neglecting friction and drag, calculate the skier's acceleration. Explain and justify any measurements, assumptions, approximations you make.

Homework Equations

F=ma

The Attempt at a Solution

I've tried a number of different things.

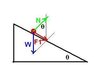
I started with a free body diagram, showing F1 moving down and to the right, w pointing straight down, and N pointing perpendicular to F1.

I then put an x y axes with the x-axis running along F1 and the y-axis along N, with W now pointing down and to the right.

I broke W into components, which didn't seem to help as I don't have enough info.
y
|N
|
|_______ x
|\ F1
| \ W
Wy | \
|_(\ <--- called this angle theta
Wx

To do that I did Cos(theta)=Wx/W
so W(cos theta) = Wx

and similary sin(theta)=Wy/W
so W(sin theta)=Wy

x | y
+F1 | +N
+W(costheta)| -w(sintheta)

I can find that N = W(sin theta) by doing

Fynet = may
ay = 0
so Fynet = 0
N - W(sintheta) = 0
N = W(sintheta)

To solve for Fxnet all I can get is
Fxnet = may
F1+W(cos theta)=max
so (F1+W(costheta))=ax

As you can see I'm pretty confused, I don't feel like that's the right answer and that I'm missing something.

 

[benjaminwhite]

Sorry, I didn't realize my crude graphs would get garbled.

. y
. |N
. |
. |_______ x
. |\ F1
. | \ W
. Wy | \
. |_(\ <--- called this angle theta
. Wx. x | y
. +F1 | +N
+W(costheta)| -w(sintheta)

 

[ehild]

Try to draw a figure with Paint or any drawing program and attach. ehild

 

[benjaminwhite]

OK, should've attached physics.JPG

 

[benjaminwhite]

and the other

 

[ehild]

Well, I am also confused, about your figures. The skier is moving downhill, does he? The forces in the free body diagram are usually drawn with respect to the slope. Is F1 the resultant downhill force?

I just show the usual figure. The skier is considered as a point mass. W is its weight, N is the normal force the slope acts on it. The vector sum of W and N is F1, and it is parallel to the slope. You have to calculate the magnitude of F to get the acceleration.

ehild

 

[benjaminwhite]

Yes, that's how my initial FBD looks. I tilted it so only W would need to be broken into components.

When I leave it as is I can break N and F1 into components but I can't get any real number without an angle can I?

 

[ehild]

You have to break W into components which are parallel and normal to the slope. You have the angle theta in the right triangles shown in the figure. The normal component of the weight cancels with the normal force of the slope. The parallel component accelerates the skier downhill.

 

[benjaminwhite]

Ahhhh ha, I think I've finally got it. Thanks very much for your patience ehild.

So
F1= 77kg*20m/s = 1540
W= 77kg*9.8m/s = 754.6

sintheta= 754.6/1540 = 0.49
arcsin0.49= 29.34

wx = 754.6(sin29.34) = 369.74

wx = 370

a = 370/77 = 4.8meters per second

 

[ehild]

NO. You need the component of force along the incline to get the acceleration from Newton's second law, F=ma.

What you calculated, mv it is the momentum of the skier. The unit of momentum is kgm/s. The acceleration is m/s^2. g, the gravitational acceleration, is 9.8 m/s^2. The unit of force is Newton, N=kgm/^2. The weight of the skier is 77*9.8= 754.6 N. If you do not know the angle of the slope you can not calculate the acceleration. You need the force along the slope, but you can not get it without knowing the angle of the slope.
What was the original text? It refers to measurement you make. You can measure the length of the slope and the time the skier travels it from the top to bottom. Or you can get the acceleration if you know the length the skier traveled from the top and the instantaneous velocity. Read the text of the problem once more.

ehild

 

[benjaminwhite]

I wish I would've realized that quite a few hours ago. I assumed the slope was 45 degrees and that makes things much easier. Thanks! :)