Amitayas Banerjee
- 31
- 2
- Homework Statement
- A tennis ball falls at velocity v onto a heavy racket
and bounces back elastically. What does the racket’s velocity
u have to be to make the ball bounce back at a right angle to
its initial trajectory and not start spinning if it did not spin
before the bounce? What is the angle β between ⃗u and the
normal of the racket’s plane, if the corresponding angle for ⃗v is α?
- Relevant Equations
- For elastic collision, the relative velocities of approach and separation along the line of impact must be same.
My approach:
Let us take two orthogonal axes: x, parallel to the racket's plane and y, perpendicular to it. For the ball to not spin, the components of initial velocities of the racket and the ball along x-axis must be same. Also, as the line of collision is along the normal to the racket's plane, the initial and final velocity components of the ball along x-axis are same.
Therefore, initial velocity of the ball: $$|v|\sin \alpha \space i - |v|\cos \alpha \space j$$
and final velocity:
$$|v|\sin \alpha \space i+(|v|\cos \alpha + 2|u| \cos \beta)j$$
Also, as the components of initial velocities of the racket and the ball along x-axis must be same,
$$|u|\sin \alpha = |u| \sin \beta$$.
Now, as the initial and final velocities of the ball are perpendicular,
$$(|v|\sin \alpha \space i - |v|\cos \alpha \space j)⋅(|v|\sin \alpha \space i+(|v|\cos \alpha + 2|u| \cos \beta)j)=0$$
I am unable to proceed. What to do next?
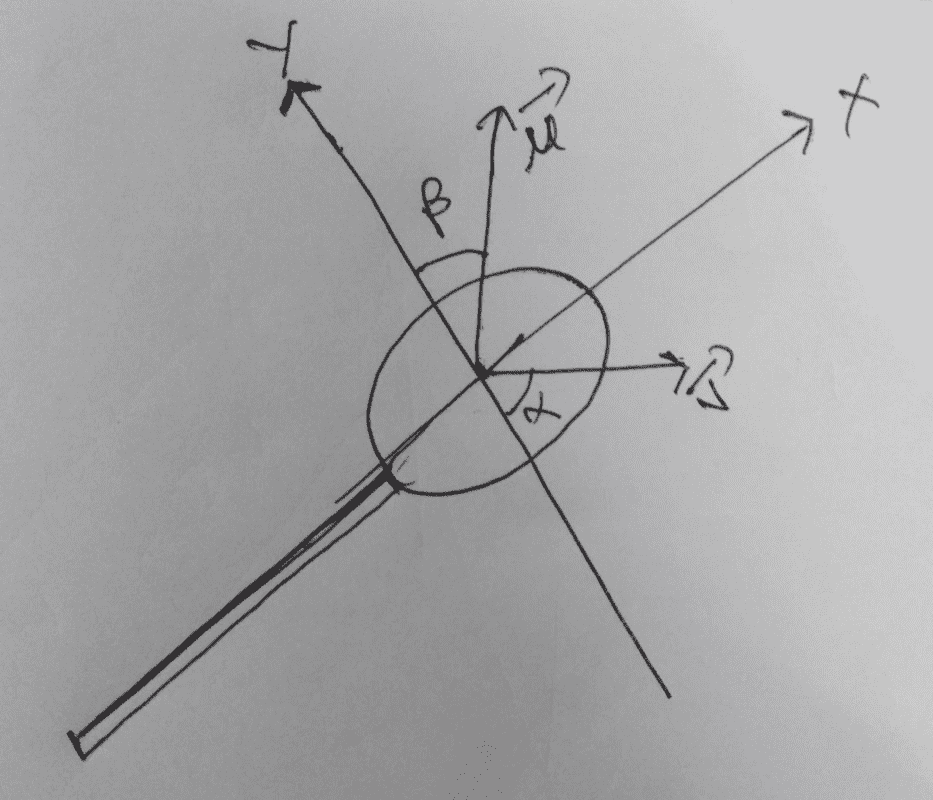
Let us take two orthogonal axes: x, parallel to the racket's plane and y, perpendicular to it. For the ball to not spin, the components of initial velocities of the racket and the ball along x-axis must be same. Also, as the line of collision is along the normal to the racket's plane, the initial and final velocity components of the ball along x-axis are same.
Therefore, initial velocity of the ball: $$|v|\sin \alpha \space i - |v|\cos \alpha \space j$$
and final velocity:
$$|v|\sin \alpha \space i+(|v|\cos \alpha + 2|u| \cos \beta)j$$
Also, as the components of initial velocities of the racket and the ball along x-axis must be same,
$$|u|\sin \alpha = |u| \sin \beta$$.
Now, as the initial and final velocities of the ball are perpendicular,
$$(|v|\sin \alpha \space i - |v|\cos \alpha \space j)⋅(|v|\sin \alpha \space i+(|v|\cos \alpha + 2|u| \cos \beta)j)=0$$
I am unable to proceed. What to do next?
Last edited: