What is the angle of the hill when the box slides with constant speed?

[freshcoast]

1. Problem statement, all variables and given/known data.

A 25kg box of books is in the back of the truck. The truck-box system has frictional coefficients (static = 0.4, kinetic = 0.25). You get in the truck and begin to drive in a straight line. Under these conditions
a) After reaching your final cruising speed of 25 m/s and reach the top of long downhill section of road with a constant slope. In order to avoid a collision you tap your brakes, and the box slips and then slides towards the front of the truck with a constant speed. What is the angle of the hill?

b) As you drive your truck over the top of a semi circular hill at a speed of 50km/hr, what is the magnitude of the maximum possible static friction force acting on the box?

2. Homework Equations .
F = ma
Vf = vo + at
X = vo^2 + 1/2at^2
Vf^2 = vo^2 + 2ax

3. Attempt at solutionFor part a) drew FBD, separated the components and moved things around to find the angle.

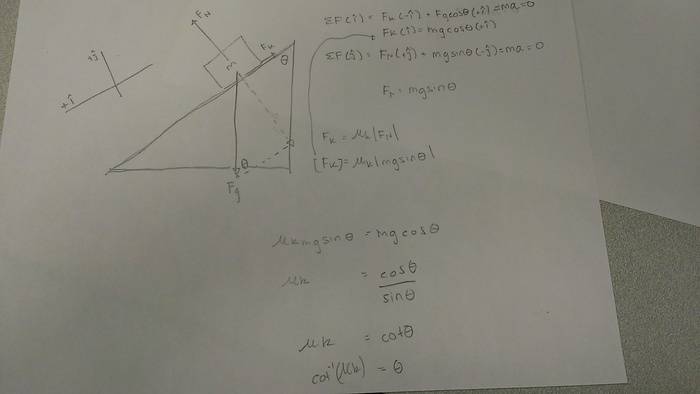
For part b) drew FBD, separated components and used the radial equation for force to find the static friction force.

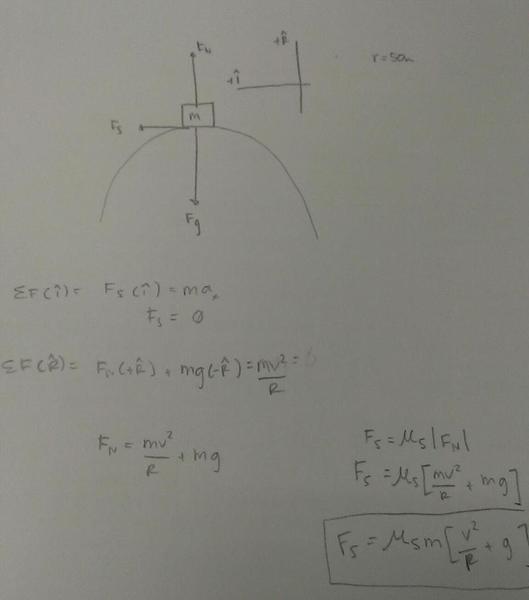
Thanks in advance for any input

 

[TSny]

I think the first part looks good.

For the second part, did you get the direction of the centripetal acceleration correct?

 

[freshcoast]

Oh no I made that mistake, thanks for pointing that out. So it would be in the -r direction meaning that the term mv^2/r would be negative thus making the normal force equal to [mg - mv^2/r] correct?

 

[TSny]

Correct.

I don't think you can assume there is no acceleration in the x direction as you go over the top of the hill. So, the part where you derive Fs = 0 might not be relevant.

 

[Nickie]

!I would like to commend you on your use of the appropriate equations and problem-solving techniques in attempting to solve this problem. It is clear that you have a good understanding of the concepts involved.

For part a), I would suggest also considering the conservation of energy principle. Since the box is sliding with a constant speed, the work done by the kinetic friction force must equal the change in potential energy of the box as it moves down the hill. This can help you find the angle of the hill more accurately.

For part b), you can also use the equation for centripetal force (F = mv^2/r) to find the maximum possible static friction force. This is because at the top of the hill, the box will experience both the centripetal force due to its circular motion and the static friction force holding it in place on the truck.

Overall, your approach to this problem is sound and with some additional considerations, you should be able to arrive at the correct solutions. Keep up the good work!