annao
- 3
- 0
Homework Statement
A plank of wood sits on top of two rollers with radius of 44.4 cm. The plank is pulled forward so it moves at a constant acceleration of 2.24 m/s^2, starting from rest, and the rollers roll without slipping along the ground and in contact with the plank. What is the angular speed of the rollers after 1.14 s? Express your answer in rad/s.
Homework Equations
w=wo+
The Attempt at a Solution
wo=0 rad/s; t=1.14 s; a=2.24 m/s^2; r=0.444 m
w=wo+
w=5.75 rad/s
Am I on the right track? Do I need to divide by 2 because there are two rollers?
Thank you
Attachments
-
 Rollers.png4.4 KB · Views: 348
Rollers.png4.4 KB · Views: 348 -
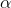 media%2Ffe6%2Ffe688a78-1523-4a26-89e0-03c6816c6024%2F49a6e28c-9948-4ec2-84cb-e0ffc07e1ff9.png187 bytes · Views: 296
media%2Ffe6%2Ffe688a78-1523-4a26-89e0-03c6816c6024%2F49a6e28c-9948-4ec2-84cb-e0ffc07e1ff9.png187 bytes · Views: 296 -
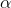 media%2Ffe6%2Ffe688a78-1523-4a26-89e0-03c6816c6024%2F49a6e28c-9948-4ec2-84cb-e0ffc07e1ff9.png187 bytes · Views: 308
media%2Ffe6%2Ffe688a78-1523-4a26-89e0-03c6816c6024%2F49a6e28c-9948-4ec2-84cb-e0ffc07e1ff9.png187 bytes · Views: 308 -
 media%2Ffe6%2Ffe688a78-1523-4a26-89e0-03c6816c6024%2F49a6e28c-9948-4ec2-84cb-e0ffc07e1ff9.png187 bytes · Views: 289
media%2Ffe6%2Ffe688a78-1523-4a26-89e0-03c6816c6024%2F49a6e28c-9948-4ec2-84cb-e0ffc07e1ff9.png187 bytes · Views: 289 -
 media%2Ffe6%2Ffe688a78-1523-4a26-89e0-03c6816c6024%2F49a6e28c-9948-4ec2-84cb-e0ffc07e1ff9.png187 bytes · Views: 333
media%2Ffe6%2Ffe688a78-1523-4a26-89e0-03c6816c6024%2F49a6e28c-9948-4ec2-84cb-e0ffc07e1ff9.png187 bytes · Views: 333