jljarrett18
- 15
- 0
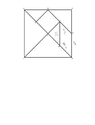
I am working on a task right now. I am currently trying to find the area of a parallelogram. I do not have the height. I only have the dimensions. I have tried suggestions like dividing the parallelogram into triangles and doing 1/2bh. The dimensions I have are the 1/2,1/2,\sqrt{2}/4, \sqrt{2}/4. I have attached a picture of what I am working on. View attachment 2736