What Is the Area of This Complex Shape?

  • Thread starter Thread starter p3rf3ct4u
  • Start date Start date
  • Tags Tags
    Area Shape
AI Thread Summary
To determine the area of the complex shape, first identify the arc as part of a circle and calculate the angle alpha from the provided diagram. Next, derive angle beta, which will help in calculating the area of the circular segment. The total area can be found by adding the area of the triangle to the circular segment area. Utilizing symmetry can simplify the calculation of the total area. This method provides a structured approach to solving the physics problem.
p3rf3ct4u
Messages
1
Reaction score
0
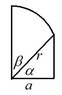
hi guys I'm doing a physics problem and it requires me to know the area of the following shape:

http://img.photobucket.com/albums/v89/p3rf3ct4u/a.jpg"

any help would be greatly appreciated!
 
Last edited by a moderator:
Physics news on Phys.org
Welcome to PF.

I think the problem could be solved as follows:

Assuming the arc is a part of a circle (which is sort of implied by the picture), first calculate the angle \alpha in my attached diagram. Then you can also find \beta and from that you can get the area of the circle segment. Then you can find the area of the total piece (by adding the triangle part) and use symmetry to find the total area.
 

Attachments

  • shape.jpg
    shape.jpg
    3.5 KB · Views: 425

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Calculate the area of this pond with functions given for the perimeter
Replies
2
Views
741
Calculating Area & Direction of Magnetic Field
Replies
9
Views
2K
Concept of Hidrostatic Pressure in Random Shaped Vessel
Replies
2
Views
1K
How do scientists use water Cerenkov detectors to detect neutrinos?
Replies
14
Views
1K
Average distance between asteroids in the asteroid belt
Replies
4
Views
2K
How Does Young's Modulus Differ from Spring Constant in Shape and Geometry?
Replies
10
Views
6K
How to find the maximum induced current for a diamond-shaped loop?
Replies
1
Views
2K
Velocity of wind based on the shape of a smoke trail
Replies
16
Views
2K
IB Extended Essay research project on relativity
Replies
13
Views
3K
Physics Extended Essay about Gauss' law and/or Lorentz force
Replies
4
Views
1K

Hot Threads

Recent Insights

Back
Top