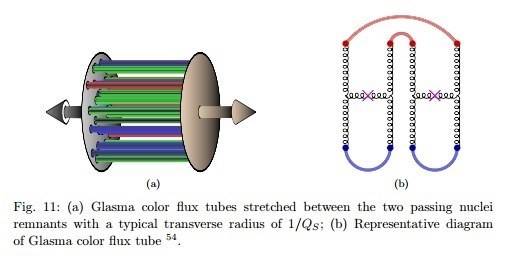
Well, this is a cartoon which is somewhat popular in the heavy-ion community. We draw disks for the colliding nuclei, because we consider them as highly Lorentz contracted, which is of course true, but you'd never see them like this "pancakes", because you have to take into account also the retardation effects of the light emitted from the object, and doing so this leads to a rotation rather like seeing Lorentz contracted objects. This was made clear already in the early 50ies by Weisskopf. If needed, I can find the reference.
Put this aside, the cartoon is pretty intuitive. The colored bars represent the very strong color fields. Due to confinement, which is a non-perturbative phenomenon, the force doesn't behave as naively expected from a massless vector field. In QED you'd have some Coulomb force, but the electromagnetic interaction is not confining, because the photons are not charged themselves. The gluons, as the quanta of the color-gauge field in QCD, themselves carry color charges, which leads to the completely different behavior. If you have two (heavy) quarks, you have to overcome a strong force, which is described by a potential like
$$V_{\text{eff}}(r)=-\frac{k}{r}+\sigma r.$$
The latter term is non-perturbative and the picture is that color flux tubes form, leading to the string tension ##\sigma##. Phenomenologically if you try to pull quarks within a hadron appart, you'll not be able to separate them and observe just free quarks but you need to put more and more energy into the system to overcome the string tension. At one point the strings break, and you create more colorless hadrons instead of freeing the quarks. This is roughly what's intended to be depicted by these colored flux tubes.