Drao92
- 70
- 0
Homework Statement
Hi guys,
Im new here and I am working for the first time with with these applications.
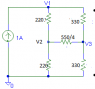
So, i have this resistor network https://www.physicsforums.com/attachment.php?attachmentid=44965&stc=1&d=1331497208 where R1=220 ohm and R2=330 ohm.
I must find the electrical resistence between pins 1-8, 1-2 and 2-4. They must give me around 92 ohm, 168 ohm and 265 ohm.
The Attempt at a Solution
For 1-8 i made (R1+R2)/6=91.66 ohm but for the others i don't know how to solve them. Ill be very glad if you`ll explain me 1-2 or 2-4 to understand how to solve these kind of problems.
PS: The resistors are not isolated, i also don't know what this means.
Well, for 1-2 i made ((R1+R2)/5+R1)*R2/(((R1+R2)/5+R1)+R2=165 ohm
Attachments
Last edited: