lIllIlIIIl
- 7
- 5
Can't figure it out, here's a screenshot with better typography.
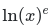
The discussion centers on finding the derivative of the function \( (\ln(x))^e \), where \( e \) is a real number. Participants emphasize the importance of clarity in the problem statement, distinguishing between \( \ln[x^e] \) and \( (\ln(x))^e \). The Chain Rule is highlighted as a crucial tool for solving the derivative, and there is a suggestion to substitute \( \ln(x) \) with \( y \) to simplify the process. Integral tables are mentioned, but they do not provide a solution for this specific derivative problem.
PREREQUISITESStudents studying calculus, educators teaching derivatives, and anyone seeking to clarify the application of the Chain Rule in complex functions.
Often integral tables can help get an answer but they are acceptable when its a homework assignment. I looked at a few and this integral is not listed. They do show ones where ##ln(x)^n## with n an integer but none with a real number power.I can't imagine where that function came from, but the chain rule is your friend!lIllIlIIIl said:Can't figure it out, here's a screenshot with better typography.
View attachment 331333
Your problem is ambiguous, so isn't clear to me.lIllIlIIIl said:Can't figure it out, here's a screenshot with better typography.
View attachment 331333
The problem asks for the derivative, not the integral.jedishrfu said:One attack that might work is to replace ln(x) with y and ask what is the integral for that