What is the effect of multiple forces on a 2D rigid rectangle?

[Droctagonopus]

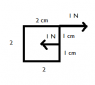
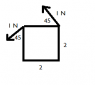
Say I have a rectangle of width w and height h centred at (0, 0) on a 2D coordinate plane.
The rectangle is free to move on a frictionless medium. It is not attached at any point.

Case 1: A single force F = (Fx)i + (Fx)j acts at a point (x, y)
How does the rectangle move? I looked it up on some websites and I think that the tangential component of the force rotates the rectangle around it's centre of gravity and the parallel component of the force causes translational motion. Is this correct?

Case 2: Multiple forces F1, F2, ..., Fn act on points (x1, y1), (x2, y2), ..., (x3, y3)
I have searched everywhere for a solution to this problem but I cannot find it. Is there a way to figure out mathematically how the rectangle rotates and/or translates?

Is there a general method to figure out the rotational and translational motion in both cases?

 

[Doc Al]

Case 1: A single force F = (Fx)i + (Fx)j acts at a point (x, y)
How does the rectangle move? I looked it up on some websites and I think that the tangential component of the force rotates the rectangle around it's centre of gravity and the parallel component of the force causes translational motion. Is this correct?

Partly right. The main error is in thinking that only the "parallel" component contributes to translational acceleration. Not so: The entire net force will determine the translational acceleration of the center of mass.

For rotation about the center of mass, consider the torque about that point from each force. Use that to determine the rotational acceleration about the center of mass.

Case 2: Multiple forces F1, F2, ..., Fn act on points (x1, y1), (x2, y2), ..., (x3, y3)
I have searched everywhere for a solution to this problem but I cannot find it. Is there a way to figure out mathematically how the rectangle rotates and/or translates?

See my comments above.

Is there a general method to figure out the rotational and translational motion in both cases?

Yes. See my comments above.

Realize that as the body moves and rotates, the torques and thus the rotational acceleration changes.

 

[Droctagonopus]

But does the rectangle always rotate about its center or mass? Remember, the rectangle is not fixed. It's free to move. It's like a rectangular plate floating freely through 2D space.

I've attached an example. In this case, would the square still rotate around it's centre of gravity because common sense doesn't say so. Although common sense has proven wrong quite a lot of times in Physics.

 

[Droctagonopus]

And also, yes, in the case of a single force, the whole force does contribute but if we were to calculate the acceleration vector of the centre of mass then we would use a = F/m where F is the parallel component of the force, right?

 

[Doc Al]

But does the rectangle always rotate about its center or mass? Remember, the rectangle is not fixed. It's free to move. It's like a rectangular plate floating freely through 2D space.

You can always treat the motion of a body as the sum of the translational motion of its center of mass plus its rotation about the center of mass. "Rotating about its center of mass" does not mean that the center of mass remains fixed.

I've attached an example. In this case, would the square still rotate around it's centre of gravity because common sense doesn't say so. Although common sense has proven wrong quite a lot of times in Physics.

The forces shown in your diagram indicate that there will be rotational acceleration about the center of mass. (We are talking about the instantaneous acceleration at the moment the square and the applied forces are as shown. Things change as time goes on.)

Why do you think it won't rotate about its center of mass?

 

[Doc Al]

And also, yes, in the case of a single force, the whole force does contribute but if we were to calculate the acceleration vector of the centre of mass then we would use a = F/m where F is the parallel component of the force, right?

No.

To find the acceleration of the center of mass you would use the entire force, not just one component.

In your diagram above, what do you think the instantaneous acceleration of the center of mass will be?

 

[Droctagonopus]

Um. I'm unsure. The net force on the object above is zero, right? So there should be no translational acceleration of the centre of mass?

 

[Doc Al]

Um. I'm unsure. The net force on the object above is zero, right? So there should be no translational acceleration of the centre of mass?

Exactly.

 

[Droctagonopus]

And the total torque of the object is the sum of the torques of each force on the object?

 

[Doc Al]

And the total torque of the object is the sum of the torques of each force on the object?

Right.

 

[Droctagonopus]

What if the net force is not zero? Then how can we figure out the translational acceleration of the object? Do we find the net force and its point of application and then find the parallel component of that?

 

[D H]

Do we find the net force and its point of application and then find the parallel component of that?

No. You find the net force and divide by mass. Period. The point of application is irrelevant as far as translational motion is concerned. The relevant equation is \vec F=m\vec a.

 

[Droctagonopus]

No no. There is both rotational and translational motion. Imagine this square is floating in 2D space with only these forces acting on it. There is both rotational and translational acceleration, right?

 

[Doc Al]

What if the net force is not zero? Then how can we figure out the translational acceleration of the object? Do we find the net force and its point of application and then find the parallel component of that?

Use the full net force and Newton's 2nd law. (Stop with the parallel component already!)

 

[Doc Al]

No no. There is both rotational and translational motion. Imagine this square is floating in 2D space with only these forces acting on it. There is both rotational and translational acceleration, right?

Not given the forces in your diagram. The net force is zero, thus the translational acceleration of the center of mass at that moment is zero.

 

[Droctagonopus]

I don't understand. In the diagram, how is it possible for the square to not rotate? Doesn't the square have both a translational and rotational acceleration?

 

[Doc Al]

I don't understand. In the diagram, how is it possible for the square to not rotate?

Who says it doesn't rotate?

Doesn't the square have both a translational and rotational acceleration?

No. What's the net force on it, according to your diagram. (You've already answered that. Stick to it.)

 

[Droctagonopus]

Okay. I think I understand the translation. What about the rotation? Does it rotate around the centre of mass? Or another point?

 

[D H]

What about the rotation? Does it rotate around the centre of mass? Or another point?

Yes.Pick any fixed point on your rigid body. A corner, the middle of a side, the center of mass. Regardless of your choice, you can *always* describe the motion of a rigid body as a combination of the translation of that selected point and a rotation of the body about that point.

The math is going to be easier with some choices. The center of mass is convenient because its the choice that decouples translational and rotational motion. Another convenient choice is the point about which motion is purely rotational. Things get hairy otherwise. That doesn't mean that its invalid. It just means that describing the motion is more complex.

 

[Droctagonopus]

If we choose any arbitrary point, the net force acts on that point and the moment is around that point. But will the motion be the same regardless of the point chosen?

 

[Droctagonopus]

What about this case? In this case the net force should be directed to the left. But from the diagram it seems like the square has only rotational acceleration.

 

[Doc Al]

What about this case? In this case the net force should be directed to the left.

Yes, the net force is to the left.

But from the diagram it seems like the square has only rotational acceleration.

Why do you think that?

 

[Droctagonopus]

I'm sorry. I get it now.

To sum up:
To find the instantaneous translational acceleration of the centre of mass of the square I find the net force F and the acceleration a = F/m.
To find the instantaneous angular acceleration around the centre of mass of the square I find the sum of the torques of each force around the centre of mass.

And this method works for any number of forces.

 

[D H]

Excellent, except that torque is the equivalent of force. You need to divide torque by the moment of inertia about the center of mass to get angular acceleration.

This approach for rotational behavior only works with 2D objects and simplified 3D problems. The general 3D problem is trickier. For one thing, moment of inertia is now a second order tensor rather than a scalar. For another, Euler's equations come into play. An object with no external torques can undergo angular acceleration. Angular momentum is a conserved quantity. Angular velocity is not.To answer your previous question, "If we choose any arbitrary point, the net force acts on that point and the moment is around that point. But will the motion be the same regardless of the point chosen?" -- That depends on what you mean by the same. Suppose a pure torque (net force = 0) is applied to your rectangle. From a center of mass perspective, the center of mass doesn't move and the object begins rotating about the center of mass. Choose some other point, say a corner. With this selection, the corner is translating and the object is rotating about the corner.

However, suppose at any point in time you plot the position and orientation of the rectangle as a whole (e.g., plot the rectangle's outline). Now both choices will yield the exact same result. If they don't it means a math error was made in least one of the approaches. Choosing a point as the point of interest doesn't change what the object really does. All choice must yield the same result. What that means is that the mathematics can be quite hairy for some choices.

 

[Droctagonopus]

Okay. Thanks a bunch for helping me understand. I'm programming a simulation for a rocket in zero gravity and needed to know an algorithm friendly method of calculating the angular and translational acceleration. Thanks.

 

[D H]

I suggest you keep it to a 2D simulation at the start. Three dimensional behavior is a much tougher nut to crack. Getting realistic 3D behavior for a real rocket is a monumental task.