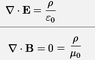- #1
userunknown
- 11
- 0
There is an analogy between electric and gravitational potential energy.
## U_g = \frac {GmM}{r}##
## U_e = \frac {kqQ}{r}##
What is the analogous formula in magnetostatics?
Thanks...
## U_g = \frac {GmM}{r}##
## U_e = \frac {kqQ}{r}##
What is the analogous formula in magnetostatics?
Thanks...