Homework Help Overview
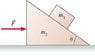
The discussion revolves around finding an expression for the magnitude of the horizontal force acting on a block on a frictionless wedge, ensuring that the block does not slip. The problem involves concepts from dynamics and forces acting on inclined planes.
Discussion Character
- Exploratory, Mathematical reasoning, Assumption checking
Approaches and Questions Raised
- The original poster attempts to relate the acceleration of the block to the horizontal force, questioning how to proceed after establishing that the block and the force must have the same horizontal acceleration. Other participants suggest setting up free body diagrams and applying Newton's second law to analyze forces in both horizontal and vertical directions.
Discussion Status
Participants are actively engaging with the problem, with some providing guidance on setting up equations based on free body diagrams. There is a recognition of the need to reconsider the components of forces and the relationship between the blocks' accelerations. The original poster expresses uncertainty about their calculations, indicating ongoing exploration of the problem.
Contextual Notes
There is mention of the conditions that all surfaces are frictionless, and the need for the blocks to accelerate together. Some participants question the dependence of the final expression on the angle theta, suggesting that this aspect requires further clarification.