uchicago2012
- 74
- 0
Homework Statement
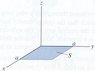
Calculate the surface flux integral of F = 2xy xhat + (xz - 5xy2)zhat over the surface shown in the figure. Take n = k.
See Figure
Homework Equations
Flux = Integral (Electric Field * dA)
The Attempt at a Solution
So from the figure the total area is obviously a2. The problem says the "surface flux integral" so I assumed they want the flux? For which you need to integrate what? Just integrating what they gave me seems wrong. I'm a bit confused about what was given and what is wanted. And I have no idea what n = k means, unless they mean the normal vector can be considered the z axis, which would make sense. But I'm still at a loss of what exactly I'm integrating.