What is the Formula for Calculating the Length of a Hanging Spring?

[erobz]

Trying to derive the length of a spring hanging under its own weight. I was trying to approach it like a series of small springs free length $l$ connected in series, in hope to use a limit as $l \to 0$ to get the final result, but either I'm bungling it, or it just doesn't work.

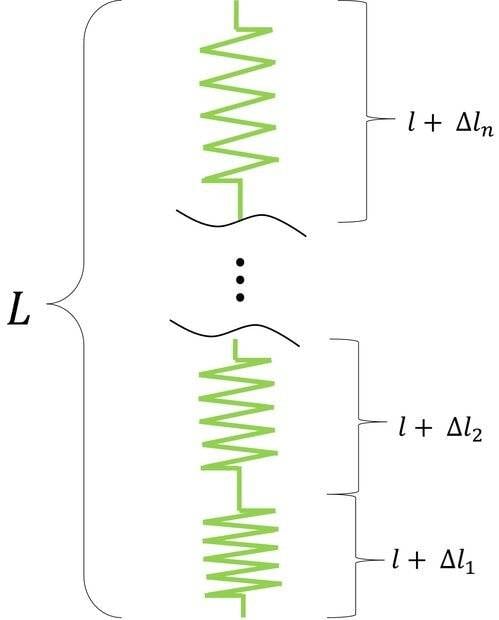
I'm proposing that the total length $L$ is given by:

$$ L = \left( l + \Delta l_1 \right) + l + \left(\Delta l_2 \right) + \cdots + \left( l + \Delta l_n \right) $$

And the force balance on each spring yields:

$$ \Delta l_n = \left( n-1\right)\frac{mg}{k} $$

Where:

$n$ is the number of springs in series

$m$ is the mass of each spring

$k$ is the spring constant

So it seems like:

$$ L = ln + \frac{mg}{k}\sum\left(n-1\right) = ln + \frac{n m g}{2 k} \left( n-1\right) $$

I do the following substitutions:

$L_o = l n$ The initial free length of the system of springs.

$m = \frac{M}{n}$ $M$ is the total mass if the spring system.

I'm left with:

$$ L_o + \frac{Mg}{2k} \left( n-1\right) $$

This is where I have an ""uh-oh" moment (perhaps I should have had it sooner)?

Any help correcting my course is greatly appreciated.

 

[Steve4Physics]

Haven't fully checked your working but don't forget that the spring-constant (k) for each mini-spring is a function of its length.

E.g. if you take a spring of spring-constant k and cut it into two equal lengths, then the spring-constant of each half is 2k.

 

[erobz]

E.g. if you take a spring of spring-constant k and cut it into two equal lengths, then the spring-constant of each half is 2k.

I don't understand that.

However, I wasn't cutting the springs though? I thought I was just making them smaller, and adding more of them.

 

[malawi_glenn]

Think about this. Two springs with identical spring constant. What is their total spring constant when coupled in series?

 

[erobz]

Think about this. Two springs with identical spring constant. What is their total spring constant when coupled in series?

$$ k_{eff} = \left( \frac{1}{k}+ \frac{1}{k} \right)^{(-1)} = \frac{1}{2} k $$

So then if I have $n$ little springs in series my spring constant is not $k$ like I think, but$\frac{k}{n}$

 

[Orodruin]

Haven't fully checked your working but don't forget that the spring-constant (k) for each mini-spring is a function of its length.

E.g. if you take a spring of spring-constant k and cut it into two equal lengths, then the spring-constant of each half is 2k.

This. It solves the OP’s issues as the limit of $n\to \infty$ becomes well defined. To offer an equivalent, but somewhat rearranged view: Hooke’s law can be written on the form $F = -\kappa \epsilon$ where $\epsilon$ is the strain, ie, elongation per length ($\Delta L/L_0$ for an ideal spring) and $\kappa$ is the normalised spring constant $kL_0$.

A small element of unstrained length $dx$ therefore has length $(1+\epsilon)dx = (1-F/\kappa)dx$. Insert the weight ($F =-m(x)g$ where $m(x)$ is the mass below $x$) and integrate.

 

[Orodruin]

$$ k_{eff} = \left( \frac{1}{k}+ \frac{1}{k} \right)^{(-1)} = \frac{1}{2} k $$

So then if I have $n$ little springs in series my spring contant is not $k$ like I think, but$\frac{k}{n}$

Exactly, so to get the correct spring constant for the smaller segments you need to multiply k by n.

 

[erobz]

Ahh...Thanks Everyone

$$ L = \lim_{n \to \infty} \left( L_o + \frac{Mg}{2k} \left( 1-\frac{1}{n}\right) \right) = L_o + \frac{Mg}{2k} $$

 

[Orodruin]

There is also an intuitive argument: At the center, the spring will have the load of half the mass and therefore have half the elongation that it would have if the load was just the full mass. The elements equidistant (when unstrained) from the center will also have an average load of half the mass (eg, at the top it is the full mass and at the bottom zero) and therefore the total elongation of those two elements would also be the same as if loaded with half the mass since Hooke’s law is linear. Therefore, the total elongation of the spring hanging under its own weight will be half of that of an ideal massless spring with the same spring constant and length loaded with the full spring weight.

 

[Orodruin]

Yet another argument:
Hookes law is linear, therefore each mass of the spring $dm$ elongates the spring above it and those elongations add up. The elongation due to a mass $dm = M \, dx/L_0$ is given by $(x/L_0) g\, dm/k = xgM \, dx /(kL_0^2)$. Integrate from 0 to $L_0$ to obtain $\Delta L = Mg/(2k)$.

 

[erobz]

This. It solves the OP’s issues as the limit of $n\to \infty$ becomes well defined. To offer an equivalent, but somewhat rearranged view: Hooke’s law can be written on the form $F = -\kappa \epsilon$ where $\epsilon$ is the strain, ie, elongation per length ($\Delta L/L_0$ for an ideal spring) and $\kappa$ is the normalised spring constant $kL_0$.

A small element of unstrained length $dx$ therefore has length $(1+\epsilon)dx = (1-F/\kappa)dx$. Insert the weight ($F =-m(x)g$ where $m(x)$ is the mass below $x$) and integrate.

What is a normalized quantity? Is it something that must result from the non-dimensionalization of a variable?

 

[Orodruin]

What is a normalized quantity? Is it something that must result from the non-dimensionalization of a variable?

A properly normalised parameter is one that has the correct magnitude. In this case, normalisattion by $L_0$ has to be made such that the parameter takes the same value regardless of your $n$ if you want to assume it to be independent of bc $n$. The parameter $\kappa$ is not dimensionless. It has dimensions of force since strain is dimensionless.

 

[erobz]

A small element of unstrained length $dx$ therefore has length $(1+\epsilon)dx = (1-F/\kappa)dx$. Insert the weight ($F =-m(x)g$ where $m(x)$ is the mass below $x$) and integrate.

This was what I'd initially hoped to do, but I still don't think I get it.

You are saying ( I believe ):

$$ L = \int_0^{L_o} \left( 1 + \epsilon \right) dx \implies \int_0^{L_o} \left( 1 + \frac{m(x) g}{ \kappa } \right) dx $$

What is $m(x)$ (the function)? To get the desired result I think it has to be:

$$ m = \left( \frac{ L_o - x}{L_o} \right) M $$

Which seems to make perfect sense to me if the spring is unstretched. However, the mass distribution of the stretched spring is not proportional like that. The mass per unit length at the top is going to be less than it is near the bottom, so I am having trouble understanding why this is not relevant?

 

[Orodruin]

What is m(x) (the function)? To get the desired result I think it has to be:

m=(Lo−xLo)M

Which seems to make perfect sense to me if the spring is unstretched. However, the mass distribution of the stretched spring is not proportional like that.

This is irrelevant, as I stated, $x$ is the unstrained coordinate and consequently $m(x)$ is the mass below the unstrained position $x$.

 

[erobz]

How do we map each point of the unstretched spring to the stretched spring?

 

[Orodruin]

With this integral:

$$ L = \int_0^{L_o} \left( 1 + \epsilon \right) dx \implies \int_0^{L_o} \left( 1 + \frac{m(x) g}{ \kappa } \right) dx $$

Just change the upper integration boundary to whatever $x_0$ you want to map to a stretched position $x_0'$.

 

[erobz]

Ok, I think I'm following along now.

So $x_P = 0$ maps to $x' = 0$

and in general:

$$ x'( x_P ) \to x_P + \frac{Mg}{k}\frac{x_P}{L_o} - \frac{1}{2} \frac{Mg}{k} \left(\frac{x_P}{L_o} \right)^2 $$

Thank you for your patience.

I will try to digest your other approaches as well.

 

[erobz]

Yet another argument:
Hookes law is linear, therefore each mass of the spring $dm$ elongates the spring above it and those elongations add up. The elongation due to a mass $dm = M \, dx/L_0$ is given by $(x/L_0) g\, dm/k = xgM \, dx /(kL_0^2)$. Integrate from 0 to $L_0$ to obtain $\Delta L = Mg/(2k)$.

I'm stuck on this one.

You have a spring element of mass

$$dm = \frac{dx}{L_o} M $$

at some position below the top of the spring $x$

Are we again using the mass below the element as the weight providing the stretch $dl$?

Or is the $dm$ at the bottom of the spring and $x$ goes to the top?

It seems like its the latter:

$$ k \,dl = \frac{x}{L_o} g \, dm $$

So it seems like it is saying the stretch $dl$ at some distance $x$ from the bottom of the spring is the sum of all the individual stretches $dx$ from each mass $dm$ at point $x$?

 

[Orodruin]

Are we again using the mass below the element as the weight providing the stretch dl?

No. We are looking at the stretch caused by $dm$. The mass $dm$ will stretch the spring above it by a fraction $x/L_0$ of what the same mass would stretch the spring if it were hung at the bottom, ie, $(x/L_0)g\, dm/k$. The $x$ coordinate starts at the top here.

 

[erobz]

No. We are looking at the stretch caused by $dm$. The mass $dm$ will stretch the spring above it by a fraction $x/L_0$ of what the same mass would stretch the spring if it were hung at the bottom, ie, $(x/L_0)g\, dm/k$. The $x$ coordinate starts at the top here.

And this bit $\frac{x}{L_o}$ of mapping information comes from the linearity property of the spring?

I don't know why this part is confusing for me. If

$$k \left( x- l_o \right) = mg $$

Where is the dependency on position for $\left( x - l_o \right)$ coming from. it seems like its constant?

 

[erobz]

It seems like we get the same $dx = \frac{g}{k} dm$ no matter where we load the mass?

 

[Orodruin]

And this bit $\frac{x}{L_o}$ of mapping information comes from the linearity property of the spring?

I don't know why this part is confusing for me. If

$$k \left( x- l_o \right) = mg $$

Where is the dependency on position for $\left( x - l_o \right)$ coming from. it seems like its constant?

This post seems garbled like you edited it some times and thoughts were lost along the way.

The argument is very simple. If you hung the mass $dm$ at the bottom of the spring, the full spring would satisfy $\Delta L = g\,dm/k$ and the elongation is linear. This means that the elongation of the upper $x$ of the spring is given by $(x/L_0)\Delta L = gx \, dm/(kL_0)$. The forces acting on this upper part are the same regardless of if the mass hangs at the bottom or $x$ down the spring so the elongation must be the same. When you hang the mass $dm$ a distance $x$ down, there are no forces acting on the part below $x$ so it will therefore not be elongated at all. The elongation of the full spring due to a mass $dm$ at position $x$ from the top is therefore $gx \, dm/(kL_0)$.

It seems like we get the same $dx = \frac{g}{k} dm$ no matter where we load the mass?

View attachment 305227

No, you don’t. See above.

 

[erobz]

This post seems garbled like you edited it some times and thoughts were lost along the way.

The argument is very simple. If you hung the mass $dm$ at the bottom of the spring, the full spring would satisfy $\Delta L = g\,dm/k$ and the elongation is linear. This means that the elongation of the upper $x$ of the spring is given by $(x/L_0)\Delta L = gx \, dm/(kL_0)$. The forces acting on this upper part are the same regardless of if the mass hangs at the bottom or $x$ down the spring so the elongation must be the same. When you hang the mass $dm$ a distance $x$ down, there are no forces acting on the part below $x$ so it will therefore not be elongated at all. The elongation of the full spring due to a mass $dm$ at position $x$ from the top is therefore $gx \, dm/(kL_0)$.No, you don’t. See above.

Alright, it makes sense. My tiny brain needs to rest before I proceed to untangle the "intuitive approach".

 

[Orodruin]

Here is (yet another) approach that mixes both the approaches how much does each mass element elongate the spring and how much is each element elongate.

Consider how much the element $dm$ at $x’$ elongate the element $dx$ at $x$. The elongation will be zero if $x > x’$ (coordinate going from top of spring) and $d\xi = d\epsilon\, dx = (g\, dm/\kappa) dx = gM\, dx’ dx/(\kappa L_0)$ if $x’ > x$. Therefore, integrate the latter over $0 < x < x’ < L_0$ to get the total elongation. Depending on which integral you do first you should recover the integral of each of the other two approaches.

 

[erobz]

There is also an intuitive argument: At the center, the spring will have the load of half the mass and therefore have half the elongation that it would have if the load was just the full mass.

This argument applies to the center of the stretched spring i.e.$\frac{L}{2}$? It seems like the mass is not distributed along the length of the spring this way. I would suspect that the point which has half the remain load beneath it to be lower than $\frac{L}{2}$ on the stretched spring.

 

[Orodruin]

This argument applies to the center of the stretched spring i.e.$\frac{L}{2}$? It seems like the mass is not distributed along the length of the spring this way. I would suspect that the point which has half the remain load beneath it to be lower than $\frac{L}{2}$ on the stretched spring.

I am always referring to the unstretched spring when I talk about position on the spring.

 

[erobz]

I am always referring to the unstretched spring when I talk about position on the spring.

You get me we with that every time!

 

[Orodruin]

You get me we with that every time!

I mean, if you try to use the stretched position you are just going to make the problem harder for yourself.