MHB What is the inequality form for a decreasing curve's slope?

[Teh]

View attachment 6135
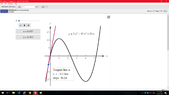
View attachment 6136They want the curve in inequality form which i am not sure if i got it right

 

[MarkFL]

We are given:

$$y=2x^3-15x^2+24x$$

Now, to determine where the slope is decreasing, we need to find where the second derivative of $y$ is negative...what do you get for $y''$?

 

[Teh]

We are given:

$$y=2x^3-15x^2+24x$$

Now, to determine where the slope is decreasing, we need to find where the second derivative of $y$ is negative...what do you get for $y''$?

y'' = 8x-15?

 

[MarkFL]

y'' = 8x-15?

We have:

$$y=2x^3-15x^2+24x$$

Now, using the power rule on each term, we get:

$$y'=6x^2-30x+24$$

And differentiating again:

$$y''=12x-30=6(2x-5)$$

So, we need to solve:

$$2x-5<0$$

What do you get?

 

[Teh]

We have:

$$y=2x^3-15x^2+24x$$

Now, using the power rule on each term, we get:

$$y'=6x^2-30x+24$$

And differentiating again:

$$y''=12x-30=6(2x-5)$$

So, we need to solve:

$$2x-5<0$$

What do you get?

$$ x < \frac{5}{2}$$

 

[MarkFL]

$$ x < \frac{5}{2}$$

Yes. (Yes)

Do you see the difference between a decreasing slope and a decreasing function? :D

 

[Teh]

Yes. (Yes)

Do you see the difference between a decreasing slope and a decreasing function? :D

No not really may you explain please

 

[MarkFL]

To find where a function is decreasing, we find the intervals in which the first derivative is negative, and to find where the slope (as represented by the first derivative) is decreasing, we naturally look at where the first derivative of the first derivative (or the second derivative of the original function) is negative. Something is negative when it is less than zero, so that's why we end up with inequalities. :D