What Is the Initial Acceleration of a Shuttle Pulled by an Elastic Cord?

[bluebear19]

Homework Statement

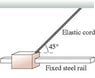
A machine has an 850g steel shuttle that is pulled along a square steel rail by an elastic cord. The shuttle is released when the elastic cord has 23.0N tension at a 45 degree angle.
What is the initial acceleration of the shuttle?

Homework Equations

F = ma
v1^2 = v0^2 + at
v1^2 = v0^2 +2a(delta x)

The Attempt at a Solution

F = ma
23 = .85a
a= 27.06 m/s^2
This is the acceleration when the cord is let go, but I have no idea how to find the inital acceleration. I know how to split the force into the x/y components but I'm not sure how that will help. Thanks

 

[chansong]

perhaps you should use Newton's second law to break the force into components:

sum of forces in x-direction = Tcos(theta) = ma_x
sum of forces in y-direction = N + Tsin(theta) - mg = ma_y = 0

Which a are you solving for? (for you to figure out)

You are given enough information from these equations and values to easily solve this I think.

 

[bluebear19]

so Fx = 23cos45 = .85a
so a_x = 19.13m/s^2

and Fy = 0
but how do these equations give you the initial acceleration? Don't they only solve for the acceleration when F = 23N

I am confused by the initial acceleration part and the part describing the string as elastic. I don't know how elasticity affects the problem. And also, should I include friction of steel on steel?

 

[tiny-tim]

Welcome to PF!

so Fx = 23cos45 = .85a
so a_x = 19.13m/s^2

and Fy = 0
but how do these equations give you the initial acceleration? Don't they only solve for the acceleration when F = 23N

I am confused by the initial acceleration part and the part describing the string as elastic. I don't know how elasticity affects the problem. And also, should I include friction of steel on steel?

Hi bluebear19! Welcome to PF!

(welcome also to chansong )

"initial" means immediately the cord is released …

in other words, while it's at its full length, and it is still at 23N tension.

So you're there! ​

(and no, you can ignore friction in any exam question that doesn't give you a coefficient of friction )

 

[bokonon]

Is the problem really this simple?

I tried solving it in this way, by finding the Fx component of the tension (23*cos45), and then dividing by the mass (.850 kg), using F=ma. However, this does not yield the correct answer. What is missing?

 

[MadhuryaRasa]

Do we need to account for steel on steel friction for this problem? I have been having such a headache with this, it is driving me crazy!

 

[bluebear19]

ok I got it, my friends helped me. so you have to find the normal force which is Fy - mg
then to find the friction force you multiply the normal force by the kinetic coefficient of friction for steel on steel. then u take that number and substract it from the Fx. then F = ma and ur done

 

[MadhuryaRasa]

Cool, thanks!

So acceleration is negative?

EDIT: Ah nvm, I've been at this way too long. Thanks again, everyone!

 

[chansong]

i was assuming there was no friction in your problem (as there was none in the one i had to solve myself)

but it looks like you've solved it so congrats