What is the kinematics of a rolling disc on a tilted plane?

[Zetor]

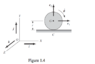
So the kinematics of the contact point of a disc rolling without slip in a Cartesian plane if fairly straightforward. The velocity for the contact point is just
v = ω r ev
where r is the wheel radius and ev the current direction vector of the wheel.

However, say that you grab the plate and force a rotation that is not around the axis around where it would roll when rolling freely on the floor. If the plate is vertical, the contact point will not change (if anything you will drill a hole in the table after while perhaps). However, if you lean the plate, this rotation will clearly induce a change of the contact point. The rate of change is largest when the plate is almost flat to the surface. Does that make sense? I could not find any visualization for this, nor did I bother to formulate this formally as I do not think it helps too much, but if you grab a plate you could probably figure out what I mean.

Where can I find a model for this kinematics? I am modeling a unicycle and no papers I have read so far consider this effect. As I could not find any full model for it yet, I guess the topic classifies as advanced. Probably the answer is related to the projection of the disc onto the plane.

 

[person_random_normal]

However, say that you grab the plate and force a rotation that is not around the axis around where it would roll when rolling freely on the floor. If the plate is vertical, the contact point will not change

can you please illustrate using an appropriate diagram...

 

[Zetor]

can you please illustrate using an appropriate diagram...

Assuming rotation only around the point G, translation of the contact point C is carried out by rotation $\dot{\theta}$. The velocity of the contact point is
$$ \dot{\vec{P}}_c =\vec {v_c}=\dot{\theta}r\vec{e}_{vc}$$

where $\vec{e}_{vc}$ is the direction vector for the velocity.

However, say that you grab on to the now vertical disc in the figure and lean it towards the floor. Then, you rotate the disc around $\vec{e}_2$. Clearly, the contact point $\vec{P}_c$ will translate although $\dot\theta =0$. The question is though, what is the kinematic model for this translation? I am looking for literature source or so covering this.

 

[A.T.]

However, say that you grab on to the now vertical disc in the figure and lean it towards the floor.

Are you talking about something like a wobbling coin? This is called Euler's Disk:
https://en.wikipedia.org/wiki/Euler's_Disk

 

[Zetor]

Well, I bet there is some paper related to the Euler Disk that can answer this. But, all I have seen regarding the Euler Disk so far are the dynamical equations for it. I am developing a model for a unicycle using Kane's method, so I basically want a kinematic model for what happens when the disc is twisted in other directions.

 

[A.T.]

Well, I bet there is some paper related to the Euler Disk that can answer this. But, all I have seen regarding the Euler Disk so far are the dynamical equations for it. I am developing a model for a unicycle using Kane's method, so I basically want a kinematic model for what happens when the disc is twisted in other directions.

To predict what will happen, you need the dynamics. Otherwise you can also dictate some kinematics, but these might not be realistic, or require additional external forces on the disk.

 

[Zetor]

Well, that is the next step. But in order to derive the dynamics, I need all kinematic relationships of the system.

 

[A.T.]

Well, that is the next step. But in order to derive the dynamics, I need all kinematic relationships of the system.

This might help:

 

[Zetor]

Well, that is a nice video but it does not single out the kinematic equations (as far as I could see). However, I think I found what I am looking for in
Advanced Engineering Dynamics by Ginsberg, at page 144. Below is a screenshot from Google Books that I found. As expected, the velocity is depending on the tilt $\theta$