What is the magnitude and direction of the electric field

In summary: So your final answer should have units of N/C.In summary, the conversation discussed finding the magnitude and direction of the electric field at a given position, indicated by a dot in a figure. The electric field was calculated using the equation kq/r^2 and the x and y components were determined for each contributing charge. The final direction and magnitude of the net electric field were found by summing the components. The proper unit for electric field is N/C.
  • #1
isukatphysics69
453
8

Homework Statement


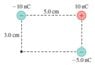
What is the magnitude and direction of the electric field at the position indicated by the dot in the figure below? Give your answer in component form in the blanks below.
phys2pic.jpg


What is the x-component of the electric field at the indicated point?

Homework Equations


kq/r^2

The Attempt at a Solution


Electric field from 1 = [(8.99x10^9)(-10x10^-9)]/((0.03)^2) = -99888.8 Nc
Electric field from 2 = [(8.99x10^9)(10x10^-9)]/((0.05830951895)^2) =26441.17 Nc
Electric field from 3 = [(8.99x10^9)(-10x-5^-9)]/(0.05^2) = -17980 NcTotal magnitude of the net electric field = sqrt((-99888.8)^2+(26441.17)^2+(-17980)^2) = 104881.8685 Nc

Now I am confused as to how to find my angle for the direction at the point in the picture. there are three different particles having an effect, if there where one id know how to find the correct angle to find the x component, but I am unsure how to get my angle here
 

Attachments

  • phys2pic.jpg
    phys2pic.jpg
    3.2 KB · Views: 1,039
Physics news on Phys.org
  • #2
I added up the vectors graphically and found the magnitude and got an angle of 252 degrees in quadrant 3. does this look correct?
 
  • #3
isukatphysics69 said:
Electric field from 1 = [(8.99x10^9)(-10x10^-9)]/((0.03)^2) = -99888.8 Nc
Electric field from 2 = [(8.99x10^9)(10x10^-9)]/((0.05830951895)^2) =26441.17 Nc
Electric field from 3 = [(8.99x10^9)(-10x-5^-9)]/(0.05^2) = -17980 Nc
Each of these field contributions has a direction. See if you can figure out each one's x and y component.
 
  • Like
Likes isukatphysics69
  • #4
Doc Al said:
Each of these field contributions has a direction. See if you can figure out each one's x and y component.
hey please see above, I added the vectors graphically on graphing paper and got 252 degrees
Doc Al said:
Each of these field contributions has a direction. See if you can figure out each one's x and y component.
So I am imagining a unit circle around the point, charge 1 has an angle of 90 degrees, charge 2 has an angle of arctan(3/5) = 30 degrees and charge 3 has an angle of 0 degrees, but then how do I find the angle on the particle?
 
  • #5
Try this: The field from the -10 nC charge (at the point in question) acts in what direction? What would be its x and y components?
 
  • Like
Likes isukatphysics69
  • #6
Doc Al said:
Try this: The field from the -10 nC charge (at the point in question) acts in what direction? What would be its x and y components?
The x component would be cos(270) = 0 and the y component would be sin(270) = -1
 
  • #7
isukatphysics69 said:
The x component would be cos(270) = 0 and the y component would be sin(270) = -1
Almost: Tell me in words which direction that field points.
 
  • #8
Doc Al said:
Almost: Tell me in words which direction that field points.
the direction of the field from charge 1 onto point P points straight down
 
  • #9
isukatphysics69 said:
the direction of the field from charge 1 onto point P points straight down
Why down? (The charge is negative.)
 
  • Like
Likes isukatphysics69
  • #10
Doc Al said:
Why down? (The charge is negative.)
am I supposed to assume that the test charge is positive?? then up. wasn't sure about what sign the test charge was
 
  • #11
isukatphysics69 said:
am I supposed to assume that the test charge is positive?? then up. wasn't sure about what sign the test charge was
No test charge is needed or mentioned. You're finding the field at a point.
 
  • Like
Likes isukatphysics69
  • #12
Doc Al said:
No test charge is needed or mentioned. You're finding the field at a point.
oh god I am confused now
 
  • #13
Hint: The field from a positive charge points in which direction: Towards or away from the charge?
 
  • Like
Likes isukatphysics69
  • #14
I thought you need a test charge to find the field at a point
 
  • #15
Doc Al said:
Hint: The field from a positive charge points in which direction: Towards or away from the charge?
away
 
  • #16
isukatphysics69 said:
I thought you need a test charge to find the field at a point
Nope. (But it can be useful to imagine one there.)

isukatphysics69 said:
away
Good. And for a negative charge?
 
  • Like
Likes isukatphysics69
  • #17
Doc Al said:
Nope. (But it can be useful to imagine one there.)Good. And for a negative charge?
towards, so it would be pointed upwards
 
  • #18
isukatphysics69 said:
towards, so it would be pointed upwards
Exactly. So the y-component would be what?

Now do the same thinking for the other charges.
 
  • Like
Likes isukatphysics69
  • #19
Doc Al said:
Exactly. So the y-component would be what?

Now do the same thinking for the other charges.
so the y component would be 99888.8sin(90) = 99888.8 Nc
 
  • #20
oh so I just sum the components
 
  • #21
So do you agree the net component for x is -4693 nC
 
  • #22
YES I GOT IT!
 
  • #23
I got 1.62/2 points isn't the unit nanocolumn?
 
  • #24
isukatphysics69 said:
I got 1.62/2 points isn't the unit nanocolumn?
I haven't checked your numbers. The proper unit for electric field is N/C (Newtons per Coulomb).
 
  • Like
Likes isukatphysics69

FAQ: What is the magnitude and direction of the electric field

What is the electric field?

The electric field is a physical quantity that describes the force experienced by an electrically charged particle in a given region of space. It is a vector quantity, meaning it has both magnitude and direction.

How is the electric field measured?

The electric field can be measured using a device called an electric field meter. This device measures the force experienced by a charged particle placed in the field and uses this information to calculate the electric field strength at that point.

What is the unit of measurement for electric field?

The unit of measurement for electric field is newtons per coulomb (N/C) in the SI system. In other systems, it may be expressed in volts per meter (V/m) or dynes per statcoulomb (dyn/statC).

How is the direction of the electric field determined?

The direction of the electric field is determined by the direction in which a positive test charge would move if placed in the field. It points away from positive charges and towards negative charges.

What factors affect the magnitude and direction of the electric field?

The magnitude and direction of the electric field can be affected by the amount and distribution of charge, as well as the distance between charges. It is also influenced by the presence of conductive materials and the dielectric properties of the surrounding medium.

Similar threads

Find the magnitude of the electric field at point P
Replies
5
Views
1K
Find electric field a distance P from a charged rod
Replies
7
Views
2K
What is the magnitude of the field at point R?
Replies
5
Views
1K
Find the Y component of Electric field at a point
2
Replies
35
Views
3K
Find the direction and magnitude of an electric field
Replies
7
Views
2K
Confused about direction of electric field
Replies
7
Views
2K
Direction of travel of a plane wave given direction of electric field
Replies
8
Views
518
What is the magnitude & direction of the eletric field?
Replies
10
Views
3K
Magnitude and DIRECTION of electric field of a square.
Replies
1
Views
6K
Find the electric field at the origin
Replies
3
Views
7K

Hot Threads

Recent Insights

Back
Top