MHB What is the measure of <ACD and how can you find it using a specific formula?

[CGuthrie91]

View attachment 2419
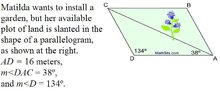
1.Find the measure of <ACD for this one i thought I'd do 180-134-38 but 8 doesn't seem right to me??
2.Find AC
3.Find AB
4.Find the area of the garden

 

[MarkFL]

It is correct, since $134+38+8=180$. :D

For the next question, I suggest the Law of Sines.

 

[CGuthrie91]

It is correct, since $134+38+8=180$. :D

For the next question, I suggest the Law of Sines.

ok so for
1. 8
2. 82.7
3.70.8
4. 1132.8

 

[Amer]

The angle is 8 degree, to find AC use the cosine law

$AC^2 = CD^2 + DA^2 - 2 (CD)(DA) \cos (134) $

After finding AC you can use law of sines

$\displaystyle \dfrac{\sin (134)}{AC} = \dfrac{\sin (38)}{CD} $

and $CD = AB$

The area of the garden is the area of the two triangles since they are the same find one and multiply with 2 the area of $CDA$
$\displaystyle [CDA] = \dfrac{(CD)(DA)\sin (134)}{2}$

 

[MarkFL]

ok so for
1. 8
2. 82.7
3.70.8
4. 1132.8

I agree with all but the last answer, but you should append the correct units to your answers, such as degrees (1) and meters (2,3) and meters squared (4).

How did you obtain your last answer?

 

[CGuthrie91]

I agree with all but the last answer, but you should append the correct units to your answers, such as degrees (1) and meters (2,3) and meters squared (4).

How did you obtain your last answer?

A=bh
So 16*70.8

 

[MarkFL]

A=bh
So 16*70.8

That formula is correct, but you are using the wrong value for $h$. Try the formula:

$$A=ab\sin(\theta)$$

where:

$$a=\overline{AD}$$

$$b=\overline{CD}=\overline{AB}$$

$$\theta=134^{\circ}$$

I recommend using the true values in the formula, and then round your final answer, rather than using rounded values in the formula. :D

 

[CGuthrie91]

That formula is correct, but you are using the wrong value for $h$. Try the formula:

$$A=ab\sin(\theta)$$

where:

$$a=\overline{AD}$$

$$b=\overline{CD}=\overline{AB}$$

$$\theta=134^{\circ}$$

I recommend using the true values in the formula, and then round your final answer, rather than using rounded values in the formula. :D

Thank you so much!