What is the Moment of Inertia of a Slender Rod in a Cable System?

[LiviaPimentel]

Homework Statement

The uniform beam shown in the IMAGE below has a weight W. If it is originally resting while supported on A and B by cables, determine the pull on cable A if cable B suddenly fails. Admit that the beam is a slender rod.
IMAGE:

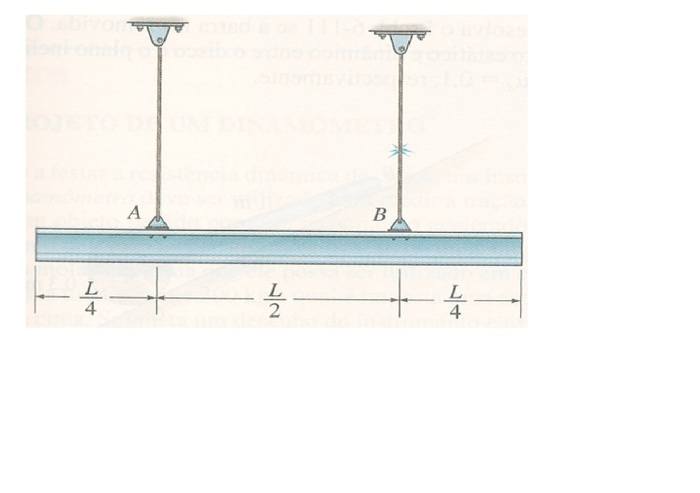
Homework Equations

TotalTorque=I*α →TotalTorque= T*L/4=I*α ; α=a/(L/4) ; in which a=acceleration of the rod

W - T = m*a

W-T = m*T*L^2/(16*I)

The Attempt at a Solution

Well, in my attempting of solving the problem, I considered that the moment of inertia utilized
in these equations is equal to m*(L^(2)/3). This is the moment of inertia of a bar that rotates around a point of its end. What I can not understand is why the teacher who provided the solution of this problem on the internet considered that I = m*(L^(2)/12), that is the moment of inertia of a bar that rotates around its center.

Can someone tell me why my way of thinking is wrong? (is it wrong?)

Thanks!

 

[Ashish Dogra]

This problem can be solved by using a basic idea that angular acceleration is same for all possible axes. If you take torque about centre and divide it by MOI about centre , that must be equal to same ratio about point of suspension.

Both axes will have either one of the forces absent from the equation.

 

[haruspex]

why my way of thinking is wrong?

You can do it either way as long as you are consistent. The axis for the MoI must be the same as the axis for the torque.
Your

T*L/4=I*α

takes the axis to be the mass centre of the rod, so that fixes the value of I to be used.
If you want to use the MoI about A then use the torque about A, WL/4.

 

[LiviaPimentel]

Thank you, Ashish Dogra and haruspex!
Now I understand it, thanks to you!

=)