gracy
- 2,486
- 83
How to recognize output voltage?I thought it is Voltage across last resistance/capacitor.
The discussion focuses on calculating the potential difference between nodes c and d in a circuit with a 100V supply between nodes a and b. The participants clarify that the equivalent capacitance calculated between c and d is incorrect because nodes c and d were lost during simplification of the circuit. The correct approach involves recognizing that the voltage source must be considered between the original nodes to determine the potential difference accurately. The final consensus is that the potential difference between c and d cannot be determined without a voltage source directly connected between those nodes.
PREREQUISITESElectrical engineering students, circuit designers, and anyone involved in capacitor circuit analysis will benefit from this discussion.
It is normally given in the problem itself.. However, the the terms input and output are commonly used in "systems" rather than in circuits like this. For example, power supply in our houses is Vin, the appliances connected to it are called 'load' and voltage across load is called output voltage.gracy said:How to recognize output voltage?I thought it is Voltage across last resistance/capacitor.
Here, R2 is the load.gracy said:Vo = I × R2
Output voltage is the voltage across "expected" or "concerned" component. In your problem, C4 is the concerned component. It is specified in the problem.gracy said:Did not understand.
Actually I copied it .gneill said:Yet now you are coming back to ask what the variables mean, and how to recognize the output? This doesn't make sense: You defined and used them yourself.
Once you are done solving a number of problems, you'll be fluent in recognizing all that stuff and mainly, conventions.gracy said:Actually I copied it .
This formula is applicable only for resistors and not capacitors. I mean, you can't simply replace R1 with C1 and R2 with C2.gracy said:I want to understand what the formula means how to use it
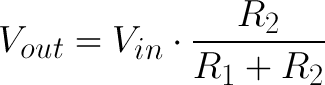
at the left side there will be voltage across the numerator on right side.
V in is always the emf of source
and denominator on the right side would be sum of all the component(resistance or capacitor) present.
numerator on the right side is always the component (resistance or capacitor) across which we want to find the voltage i.e V present on left side.
Right. For resistors and inductors.gracy said:I want to understand what the formula means how to use it
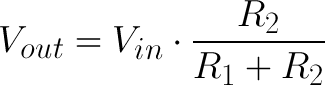
at the left side there will be voltage across the numerator on right side.
V in is always the emf of source
and denominator on the right side would be sum of all the component(resistance or capacitor) present.
numerator on the right side is always the component (resistance or capacitor) across which we want to find the voltage i.e V present on left side.
It can be source voltage but precisely, it is the total voltage across the series combination.gracy said:V in is always the emf of source
Refer to the derivation that you copied. The derivation used the fact that all the resistors in a series string share the same current. Then Ohm's law can be used with that current to find the voltage across anyone of the resistors in the string. It happened to be R2 in this example.gracy said:I want to understand what the formula means how to use it
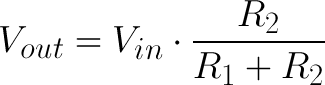
at the left side there will be voltage across the numerator on right side.
V in is always the emf of source
and denominator on the right side would be sum of all the component(resistance or capacitor) present.
numerator on the right side is always the component (resistance or capacitor) across which we want to find the voltage i.e V present on left side.
Capacitors in Series all have the same current flowing through themgneill said:Now, what is the common factor shared by all capacitors in a series string?
Right. But current ceases in steady state. What else is common?gracy said:Capacitors in Series all have the same current flowing through them
Correct for resistors and inductors and not capacitors, as I said in #70.gracy said:Please tell me am I correct in#68 that
Here in the following equation
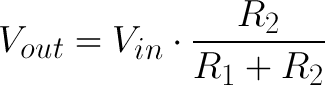
on the left side there is voltage across the numerator on right side.
V in is always the emf of source
and denominator on the right side would be sum of all the component(resistance or capacitor) present.
numerator on the right side is always the component (resistance or capacitor) across which we want to find the voltage i.e V present on left side.
See post #72.gracy said:Please tell me am I correct in#68 that...
The equivalent charge is the same as the individual charges.cnh1995 said:What else is common?
Right.gracy said:The equivalent charge is the same as the individual charges.
For how many capacitors in series? The formula will change as the number goes up.gracy said:Now how to proceed from here?
This is why it's better to understand the concept rather than try to memorize individual formulas. The concept applies to any number components in series, and a correct formula can be written down every time from the principle involved.cnh1995 said:For how many capacitors in series? The formula will change as the number goes up.
chargegneill said:Find out what is common to every component
Calculate total charge from the equation Qtotal=Ceq*V. Then simply use Vconcerned=Qtotal/Cconcerned.gracy said:Now how to proceed from here?
100 multiplied by 8μCcnh1995 said:Qtotal=Ceq*V.
You have to consider only the series combination .gracy said:100 multiplied by 8μC
800 μC=Qtotal
Right?
Right. Qtotal for the series combination.gracy said:100 multiplied by 2μC
200 μC=Qtotal
Right?
Vcd=200 μC/6μFcnh1995 said:Then simply use Vconcerned=Qtotal/Cconcerned.
Correctgracy said:Vcd=200 μC/6μF
=100/3 Volts
Right?