What is the probability of an integer being divisible by 6 or 8?

[adjacent]

Homework Statement

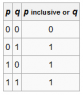
An integer is chosen random from the first 100 positive integers. What is the probability that the integer is divisible by 6 or 8?

Homework Equations

NaN

The Attempt at a Solution

The answer is 24/100 if I ignore one of the Multiples of 6 AND 8,which occurs 4 times in 100
The answer is 28/100 if I include the numbers which occur twice

What is correct here?

 

[HallsofIvy]

What do you mean by "ignore" and "count"? You certainly cannot "ignore" multiples of 24 (smallest number divisible by both 6 and 8) you just don't want to count them twice. 24/100 is correct. 6 divides into 100 16 times. 8 divides into 100 12 times. 24 divides into 100 4 times. There are 16+ 12- 4= 24 numbers less than 100 which are divisible by 6 or 8 or both.

 

[adjacent]

What do you mean by "ignore" and "count"? You certainly cannot "ignore" multiples of 24 (smallest number divisible by both 6 and 8) you just don't want to count them twice. 24/100 is correct. 6 divides into 100 16 times. 8 divides into 100 12 times. 24 divides into 100 4 times. There are 16+ 12- 4= 24 numbers less than 100 which are divisible by 6 or 8 or both.

Oh, thanks.
I have another question too.

If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9. The sum of these multiples is 23.

Find the sum of all the multiples of 3 or 5 below 1000.

The answer is 233168 according to them. But I think this is wrong.
This is the code which was used to get this answer:

int result = 0;
for (int i = 1; i < 1000; i++) {
    if (((i % 3) == 0) || ((i % 5) == 0)) {
        result += i;
    }

Obviously,if a number is a multiple of both 3 and 5, then we should add it to the result twice. However, this code does not do that. That means this is wrong.

The actual answer should be:
1000/5=200. The question asks numbers below 1000, so it should be 200-5=195. $\to$195 multiples of 5 is below 1000.
1000/3=333.333... so 333 multiples of 3 is below 1000.

Then we should sum the arithmetic sequences of multiples of 3 and 5:
$$\frac{n}{2}(a+l)$$
$$\frac{333}{2}(3+999)+ \frac{195}{2}(5+995)=264333$$
The answer is $264333$
Who is right? Me or project euler?

 

[Saitama]

Obviously,if a number is a multiple of both 3 and 5, then we should add it to the result twice. However, this code does not do that. That means this is wrong.

If a number is a multiple of both 3 and 5, it gets added to the result twice. So you should subtract the numbers which are a multiple of $\text{lcm}(3,5)=15$ because those numbers will be added twice in the sum and you get an erroneous result.

1000/5=200. The question asks numbers below 1000, so it should be 200-5=195. $\to$195 multiples of 5 is below 1000.

$199$ multiples of $5$.

Then we should sum the arithmetic sequences of multiples of 3 and 5:
$$\frac{n}{2}(a+l)$$
$$\frac{333}{2}(3+999)+ \frac{195}{2}(5+995)=264333$$
The answer is $264333$

Replace $195$ with $199$ and remember to subtract the sum of numbers which are a multiple of $15$.

 

[adjacent]

If a number is a multiple of both 3 and 5, it gets added to the result twice. So you should subtract the numbers which are a multiple of $\text{lcm}(3,5)=15$ because those numbers will be added twice in the sum and you get an erroneous result.

Oh, thanks for that 199.
I still do not understand. The question asks to Find the sum of all the multiples of 3 or 5 below 1000.
Why should we not add the multiples of 15 simply because it occurs twice?

 

[Saitama]

Oh, thanks for that 199.
I still do not understand. The question asks to Find the sum of all the multiples of 3 or 5 below 1000.
Why should we not add the multiples of 15 simply because it occurs twice?

When you add the multiples of 3, you also add the multiples of 15, right?

When you add the multiples of 5, you again add the multiples of 15. So now there are two instances of the same number getting added to the required sum. Do you see now?

 

[adjacent]

Oh , I see that the "OR" in the question is an exclusive or. But how do we determine it from the question?

 

[Saitama]

Oh , I see that the "OR" in the question is an exclusive or. But how do we determine it from the question?

Isn't that obvious? We need to count the numbers which are either a multiple of 3 or 5. So if the question asked about the numbers less than 20, then the required set of numbers would be 3,5,6,9,10,12,15,18 instead of 3,5,6,9,10,12,15,15,18.

 

[haruspex]

Oh , I see that the "OR" in the question is an exclusive or. But how do we determine it from the question?

No, it's inclusive. If it were exclusive you would not count multiples of 15 at all. It is inclusive, so you count multiples of 15 once. In neither case would you count them twice.

 

[adjacent]

No, it's inclusive. If it were exclusive you would not count multiples of 15 at all. It is inclusive, so you count multiples of 15 once. In neither case would you count them twice.

Why? This is an example of inclusive or

This becomes true even if p and q comes twice.

 

[Orodruin]

P or Q is 1 if P and Q is 1. You are treating it as if it was 2.

 

[Orodruin]

Well, in logic terms what you are doing is first summing over P=1 and then adding the sum over Q=1. This is not the same as summing over (P or Q). The sum over (P or Q) is exactly what is in the code in #3.

 

[adjacent]

Ok, I think I understand now. Thanks guys