scottlangendy
- 2
- 0
Hey guys,
I've been working on this computer application, and ended up needing to compute the roots of a quartic equation. So I implemented Ferrari's method and the results for the most part are working, however I've come across a few exceptions where I'm getting incorrect results.
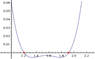
For example if I try and calculate the roots for this equation:
y = 0.9604000000000001x^4 - 5.997600000000001x^3 + 13.951750054511718x^2 - 14.326264455924333x + 5.474214401412618
It returns the following roots:
1.7820304835380467 + 0i
1.34041662585388 + 0i
1.3404185025061823 + 0i
1.7820323472855648 + 0i
When I graph the equation with a graphing calculator, I find that these are actually incorrect, and the real roots are actually closer to 1.2 and 2.9 (approximately).
The results its returning aren't totally random, they actually seem to be the results of the equations first derivative.
I tried out a bunch of root calculators online (I presume they are using the same method) and they returned the same results, so I'm pretty certain I've implemented the formula correcting.
This only seems to happen when the quartic has only two real roots, so I'm under the impression that I'm ignoring some sort of special case!
Can anyone offer me any insight as to why this is happening?
I've been working on this computer application, and ended up needing to compute the roots of a quartic equation. So I implemented Ferrari's method and the results for the most part are working, however I've come across a few exceptions where I'm getting incorrect results.
For example if I try and calculate the roots for this equation:
y = 0.9604000000000001x^4 - 5.997600000000001x^3 + 13.951750054511718x^2 - 14.326264455924333x + 5.474214401412618
It returns the following roots:
1.7820304835380467 + 0i
1.34041662585388 + 0i
1.3404185025061823 + 0i
1.7820323472855648 + 0i
When I graph the equation with a graphing calculator, I find that these are actually incorrect, and the real roots are actually closer to 1.2 and 2.9 (approximately).
The results its returning aren't totally random, they actually seem to be the results of the equations first derivative.
I tried out a bunch of root calculators online (I presume they are using the same method) and they returned the same results, so I'm pretty certain I've implemented the formula correcting.
This only seems to happen when the quartic has only two real roots, so I'm under the impression that I'm ignoring some sort of special case!
Can anyone offer me any insight as to why this is happening?