What is the required force to lift oneself using movable pulleys?

  • Thread starter Thread starter xX1SHOt
  • Start date Start date
  • Tags Tags
    Force Pulleys
AI Thread Summary
To determine the force required for a man weighing 780 N to lift himself using movable pulleys, the tension in the rope must equal half of his weight due to the mechanics of the pulley system. The initial calculation suggested that pulling with a force of 390 N would suffice, but this was incorrect. The correct approach indicates that the total tension must equal the man's weight, leading to the conclusion that he needs to exert a force of 780 N to lift himself steadily. The absence of an acceleration value in the problem complicates the calculations, but ultimately, the solution was found. Understanding the dynamics of tension in pulley systems is crucial for solving such problems effectively.
xX1SHOt
Messages
18
Reaction score
0
1. Homework Statement

In the figure below, the man and the platform together weigh 780 N. The pulley can be modeled as frictionless. Determine how hard the man has to pull on the rope to lift himself steadily upward above the ground.

p4-33.gif


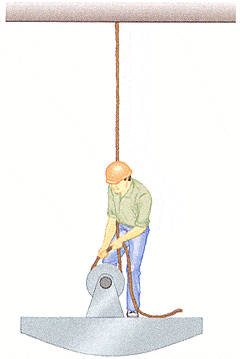
____________N



2. Homework Equations

I didn't use any until it said i was wrong but here is what it would be:

mg = T(1) + T(2)
T(1) = T(2)



3. The Attempt at a Solution

mg = 780 N = 2*T(1)

780 N / 2 = T(1)

390 N = T(1)

I first entered 390 and it was wrong, then I tried 391 to steadily move it upward. Both were wrong. Any help?
 

Attachments

  • p4-33.gif
    p4-33.gif
    11.7 KB · Views: 745
  • p4-33.gif
    p4-33.gif
    11.7 KB · Views: 495
  • p4-33.gif
    p4-33.gif
    11.7 KB · Views: 493
  • p4-33.gif
    p4-33.gif
    11.7 KB · Views: 479
Physics news on Phys.org
cant anyone help
 
I believe the answer is simply T = 780 N.

T - mg = m(0)
T = mg = 780 N

They didn't give you any value for the acceleration which if they did would've changed alot.
 
nevermind i figured it out, thanks
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Problem with pulleys - two fixed and one movable
Replies
22
Views
317
Time period of SHM & Energy conservation in pulley-spring-block system
Replies
24
Views
3K
Torque of Pulley with Two Masses2
Replies
6
Views
2K
How Does Nick's Acceleration Change When His Friend Pulls the Rope?
Replies
6
Views
3K
Person pulling themselves up a double pulley
Replies
19
Views
5K
Force applied on the pulley of a system
Replies
8
Views
3K
What is the acceleration of two masses on pulleys with constant tension?
Replies
10
Views
1K
Ball suspended by a pulley: oscillation
Replies
2
Views
1K
How do masses and pulleys behave in a balanced system with different weights?
Replies
10
Views
1K
Calculating the force for a differential pulley
Replies
20
Views
4K

Hot Threads

Recent Insights

Back
Top