Bolter
- 262
- 31
- Homework Statement
- See image below
- Relevant Equations
- Stress = force/area
Here is a MCQ which I'm struggling to answer
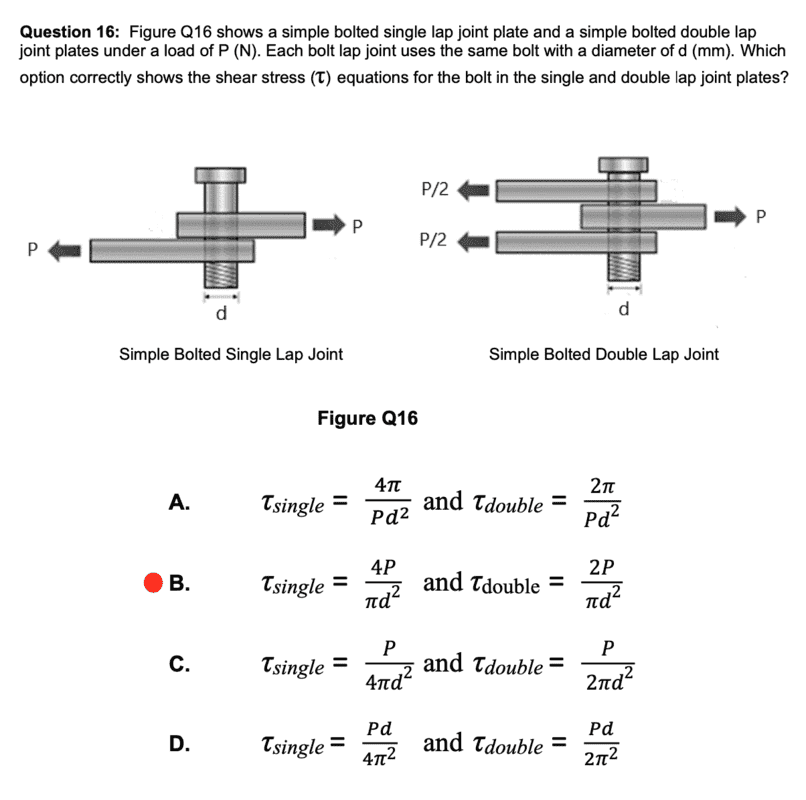
The option with a red dot is the answer I chosen and think is right
I know that stress is equal to force/area
Area i.e. the cross sectional area of a circle is (pi*d2)/4
Looking at the simple lap joint, force is simple P netwons
hence stress is P/(pi*d2)/4 giving 4P/(pi*d2)
Not so sure about the double lap joint, but I think force must be P/2 Newtons, hence stress is (P/2)/((pi*d2)/4 = 2P/pi*d2
Thus giving me option b as the answer. Is this the way you work it out?
Thanks in advance!
The option with a red dot is the answer I chosen and think is right
I know that stress is equal to force/area
Area i.e. the cross sectional area of a circle is (pi*d2)/4
Looking at the simple lap joint, force is simple P netwons
hence stress is P/(pi*d2)/4 giving 4P/(pi*d2)
Not so sure about the double lap joint, but I think force must be P/2 Newtons, hence stress is (P/2)/((pi*d2)/4 = 2P/pi*d2
Thus giving me option b as the answer. Is this the way you work it out?
Thanks in advance!