What's the difference between pushing/lifting a weight?

[Chris Lyddon]

Hi, I am working on a project where the normal process has been to push a single linear plain away from a given area. I am now considering lifting the single linear plain away but wondered about the physical dynamics when comparing pushing to lifting something.

In the image:-
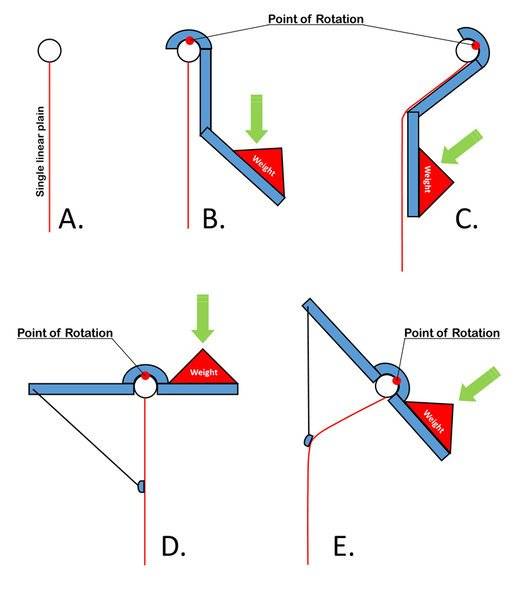
A. Represents the hanging vertical linear plain.
B. Represents a rotational cap with an angled arm. A weight is about to be applied exerting downward force.
C. Represents that downward force causing a rotation at the top and causing the single linear plain to be pushed away from the vertical.
D. Represents the same vertical linear plain but with an attachment to the centre of that plain. From the top of this central point, there is a balanced arm where a weight can be applied exerting downward force.
E. Represents that downward force causing a rotation at the top and causing the single linear plain to be lifted away from the vertical.

So, my question is, are the physical dynamics of C, different from the physical dynamics of E?

 

[jambaugh]

It appears to me that in the E case, the point at which the force is being applied is fixed along the (originally) vertical extent of the plane. (Are you bending sheet metal?) whereas the B case is permitted to slide. This could cause a relative difference in the compression/tension of the sheets above and below the point of application of force.
You'll notice that the force due to "pulling" will be in the direction of the pull because it is transmitted to the point of action using tension along what looks to me like a flexible coupling device. (cable ?) The pushing application is with a rigid body and unless it has an intentionally roughed surface for gripping I would expect it to slide allowing only forces normal to the surface of application.

Actually if that corner is sharp the force could be in any direction withing the two normals to the two faces. So the two cases become less distinct the more the plane is bent.

Could you give more details about the application without giving away your "better mousetrap"?

 

[Chris Lyddon]

Hi, thanks for your reply.

The vertical plane is a lightweight material and the function is to hold the material away from a given area. Pushing the material away defines one dynamic while lifting the material away defines another, at least, we think so.

 

[Delta2]

The final state seems to be the same in C and E (or almost the same), however I expect the dynamics that the system takes between state B and state C and between state D and state E, to be quite different. That is the forces and the velocities involved as well as how these forces and velocities change through the time during which the rotation happens must be quite different in the two cases.

However your question seems to focus on what happens in the final states C and E. The main difference i see is the surface area of the force that is applied to the plain. In the case of C the force is applied in almost the whole surface of the plain, while in the case of E the force is applied in a tiny spot . So yes the physical dynamics of C are different than the physical dynamics of E (though C and E seem to be equilibrium states so we should speak about statics here and not dynamics, but I can understand your use of word dynamics, its a dynamic equilibrium where there are forces which cancel each other). Even if we do the calculations and find out that the magnitude of force in C is the same as the magnitude of force in E, that force is applied to a tiny spot in the case of E while in C the same force is applied to a much bigger surface.​

 

[jambaugh]

I think the difference matters only if you are concerned with deformations of the planar material. Obviously it is bending to allow for the translation. If your material is sufficiently flexible then as you will see a compressive force on the top half in the second example, the material will buckle. In the first example you will have tension throughout (presuming gravity keeps it initially in tension).

[edit] of course this can be mitigated by "pulling" from a strategically placed point.

 

[Chris Lyddon]

Hi, thanks for your comment.
As the linear plane is two dimensional, then the lifting point in D/E represents a fixed point running parallel across the entire surface. The movement of the counterweight lifts the curtain cleanly away from the zone to be vacated.
On a basic level, when the human form pushes an object, different energy points are brought into play as opposed to those that are used to lift an object. I am seeking an explanation as to the difference.

 

[Chris Lyddon]

Sorry, that should read "As the linear plane is two dimensional, then the lifting point in D/E represents a fixed point running horizontally across the entire surface."

 

[jambaugh]

The critical issue is that in the latter case your point(s) of attachment are fixed. Imagine a cat clawing at a table cloth rather than the table edge pushing it.
Looking at the tension lines pulling the curtain you have both a normal and a tangential component of that pull. The normal component will move it to the side and then up a bit, the tangential component will cause the upper half to be compressed. More realistically the upper half will bend in a loop under its own weight until it is hanging down at the same angle as the tension lines are attached to it.

You would see something like this if the material is very flexable.

 

[Delta2]

What about the arm in C, does its surface match the surface of the plain?.
if that's the case then I think the internal stress forces inside the plain material will be much bigger in state E than in state C.
You might want to take a look at Wikipedia entry about stress.
https://en.wikipedia.org/wiki/Stress_(mechanics)

 

[CWatters]

I don't think D will give the result in E if the plain and suspension wire are flexible. The weight of the plain will pull the suspension wire to the right something like this...

Edit: Sorry didn't see that jambaugh had beaten me to it.

 

[Delta2]

I don't think D will give the result in E if the plain and suspension wire are flexible. The weight of the plain will pull the suspension wire to the right something like this...

View attachment 227655

Edit: Sorry didn't see that jambaugh had beaten me to it.

I think this depends not only on how flexible is the plain material but also on how heavy it is. It might be flexible enough so that it changes shape due to the force of the arm in C, but its weight might not be enough to make it bend as you say here. The OP states at a post #3 that it is a lightweight material.