Wheatstone Bridge: Substitution Resistance Formula Derivation?

[bagasme]

Hello,

In high school, I had been taught about finding substitution resistance from Wheatstone bridge.

The formula:

a. If the cross product of $R1$ and $R3$ is same as $R2$ and $R4$, the galvanometer in the middle ($R_5$) can be omitted and use series-parallel principle to solve for the substitution resistance.

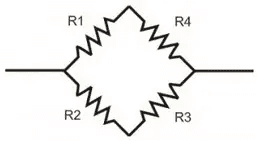
b. If instead the cross products are different, modify the circuit to the following diagram below,

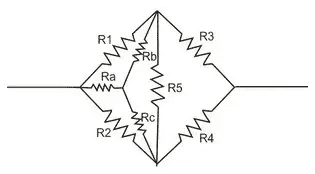
and determine new resistances ($R_a$, $R_b$, & $R_c$) by:

$$\begin{align}
R_a &= \frac {R_1 \cdot R_2} {R_1 + R_2 + R_5} \nonumber \\
R_b &= \frac {R_1 \cdot R_5} {R_1 + R_2 + R_5} \nonumber \\
R_c &= \frac {R_2 \cdot R_5} {R_1 + R_2 + R_5} \nonumber
\end{align}$$
Then, use new resistance to solve for substitution resistance.

However, there isn't any explanation or derivation of the formula AFAIK (even on my textbook).

So what derivation that lead me to the formulas above?

Bagas

 

[gneill]

A web search for "Delta Wye Transform derivation" will turn up what you need.

 

[bagasme]

But what about derivation of formula a. ?

 

[gneill]

But what about derivation of formula a. ?

I'm not sure what you mean. What is "formula a"?

There are examples of the derivation of the transformations on the web that can be readily found.

 

[Dullard]

'a' can probably be derived, but (by inspection):

R5 may be omitted from the analysis if there is no current flow through it - it isn't 'doing' anything
there is no current flow through R5 if (and only if) the voltages at either end of R5 are equal
the voltages are equal when R1/R4 = R2/R3 (or R1R3 = R2R4)
.