houlahound
- 907
- 223
looking at notes on functional analysis for self study. the authors I have stumbled across so far launch straight into the formal theory. I can't find any middle ground of intuitive motivations for the theory as yet. I am assuming the following is part of set theory? I can't follow the arguments because I don't know the terminology. are there lists defined for example the symbols in the following. I do not want these particular ones defined I want to know how to do it myself.
what branch of math do I need to read to get a foundation in this language.
any recommended readings.
thanks any leads.
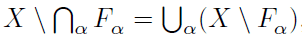
what branch of math do I need to read to get a foundation in this language.
any recommended readings.
thanks any leads.