w9537
- 7
- 1
If I put a very long steel plate above a coil with DC, the magnetic field above the plate will decrease because of the shielding of the steel plate.
However, from the perspective of magnetci domain, some domains will be magnetized to turn to the direction of the magnetic field from the coil.
Therefore, the magnetic field above should be from two source. One of them is the coil, the other is the magnetic domain in the steel plate. As a result, the magnetic field should increase rather than decreasing. But in fact, the magnetic field will decrease.
This question has puzzled me for a long time. I hope someone could help me figure it out! Thanks!
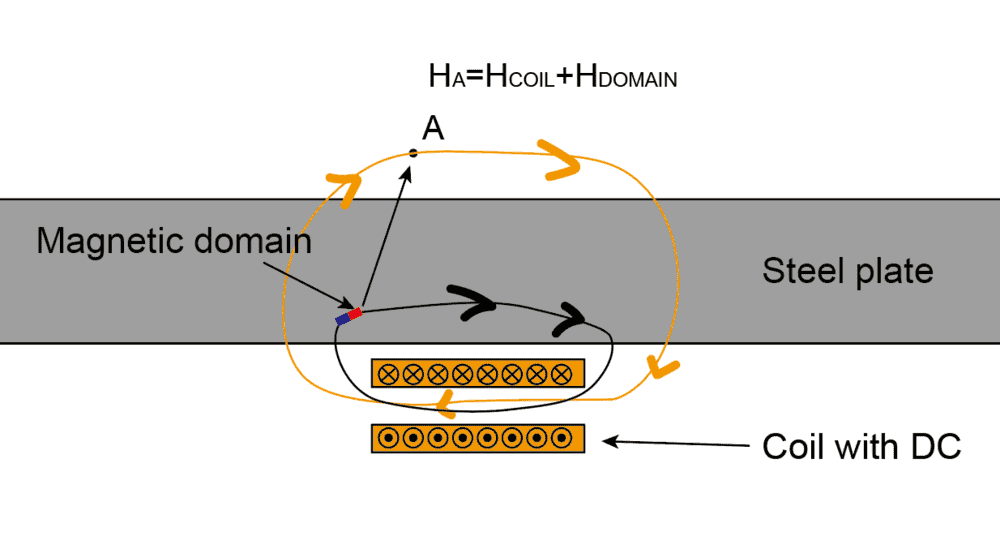
However, from the perspective of magnetci domain, some domains will be magnetized to turn to the direction of the magnetic field from the coil.
Therefore, the magnetic field above should be from two source. One of them is the coil, the other is the magnetic domain in the steel plate. As a result, the magnetic field should increase rather than decreasing. But in fact, the magnetic field will decrease.
This question has puzzled me for a long time. I hope someone could help me figure it out! Thanks!