Why are there more zeros in a sine wave than 1s and -1s?

[dexterdev]

Hello guys,
From a layman's viewpoint when we count occurrences of different amplitude values, then frequency of zeros must be maximum is not it? but it is as below:

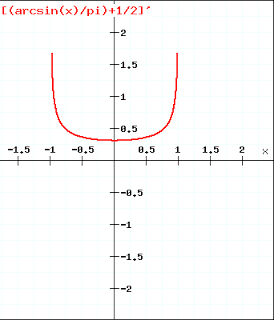
why so? zeoros must be maximum, 1s and -1s are lesser than 0 isn't it?

 

[Simon Bridge]

"frequency of zeros must be maximum"?

The zeros of a function are the roots.
Positions x: f(x)=0.

In f(t)=sin(wt) the frequency is w, the amplitude is 1, and the zeros are twice as frequent as that.

The values that |sin(wt|=1 is the same frequency as the the frequency of the zeros ... but the peaks and the troughs appear only as frequently as w.

This what you are saying?
I think you need to revisit, carefully, how the graph was derived and what it actually means. I'm not sure it is telling you what you think it does.
eg. I think the frequency of occurance of the number of points of intersection between y=f(x) and y=k is the same for every k except for |k|=1 - where it is half.

 

[haruspex]

Your question is very unclear, but your graph illustrates that a sine function spends much longer vicinity of 1 and -1 rather than in the vicinity of 0. Is that surprising?

 

[jambaugh]

Remember the slope of the inverse is reciprocal of slope of the function.
what you state is true for derivative of sine, it will be opposite for derivative of arcsine.
Especially slope of sine is 0 at (pi/2,1) so slope of arcsine approaches infinity at (1,pi/2).

 

[Simon Bridge]

Your question is very unclear, but your graph illustrates that a sine function spends much longer vicinity of 1 and -1 rather than in the vicinity of 0. Is that surprising?

Oh is that what it is - illustrating hang-time?!

 

[dexterdev]

The probability density of a steady sine-wave ' Asin (wt) ' is not
bell-shaped, since it spends more time near the peaks than near x = 0; it extends
only over -A ≤ x ≤ +A (it is zero outside that range) and spikes at the maximum
positive and negative values. (lines from moretti.ceat.okstate.edu/MAE5073/Prob1801.pdf)

but how?


These are the lines of confusion for me. My idea of pdf is that it gives peaks for higher probability values. But for a sine wave why is zeros lesser, it must be maximum. consider one cycle of sine wave. We have one peak A, one negative peak -A and 2 zeroes (3rd zero for next cycle). Is my calculus bad? If my basic idea is wrong , please can anyone kindly explain it to me (in very simple english). You people are my strength, truely.

TIA

 

[haruspex]

The probability density of a steady sine-wave ' Asin (wt) ' is not bell-shaped, since it spends more time near the peaks than near x = 0; it extends
only over -A ≤ x ≤ +A (it is zero outside that range) and spikes at the maximum
positive and negative values. (lines from moretti.ceat.okstate.edu/MAE5073/Prob1801.pdf)

My idea of pdf is that it gives peaks for higher probability values. But for a sine wave why is zeros lesser, it must be maximum. consider one cycle of sine wave. We have one peak A, one negative peak -A and 2 zeroes (3rd zero for next cycle).

For a continuous distribution, the value of the pdf at some point x cannot be interpreted as how often it takes the value x. The probability of getting exactly x is zero. Instead, think of it as the probability of getting a value in a small range about x.
If you take a thin horizontal band through a sine wave around the y=0 line, the curve doesn't spend long in the band. It enters the band every pi, but passes through quickly. A similar band at y=1 is entered half as often, but the curve spends much longer in the band each time.

 

[dexterdev]

Thankyou sir, you saved my life. I don't why doubts are haunting me like this.

Thanks again