Why can't an alpha particle be captured by the nucleus?

[rwooduk]

I understand that there are many attempts from inside the nucleus to tunnel out therefore if it was just one alpha particle trying to get in it wouldn't happen. I'm struggling with this derivation from class to describe the number of attempts:

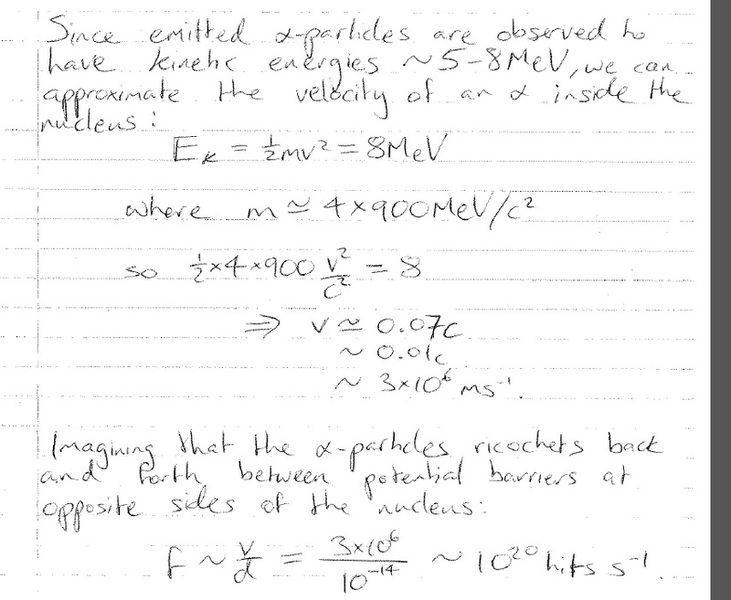
How does a velocity and size of the nucleus result in the number of hits per second? It works with dimensional analysis i.e. m/s / m = 1/s ---> frequency.

But this hits per second has been derived from a single alpha particle. I'm a little confused. Any insights on this rough derivation and an explanation would really be appreciated.

 

[rwooduk]

Oh, it ricochets back and forth, I see now. Please feel free to delete this. Although any comments are still welcome.

 

[mfb]

Oh, it ricochets back and forth, I see now.

Right.

Keep in mind that this evaluation is only a very rough approximation - there is not an actual alpha particle moving around in the nucleus as classical mechanics is not useful for systems like this.