- #1
dangerboyy
- 8
- 0
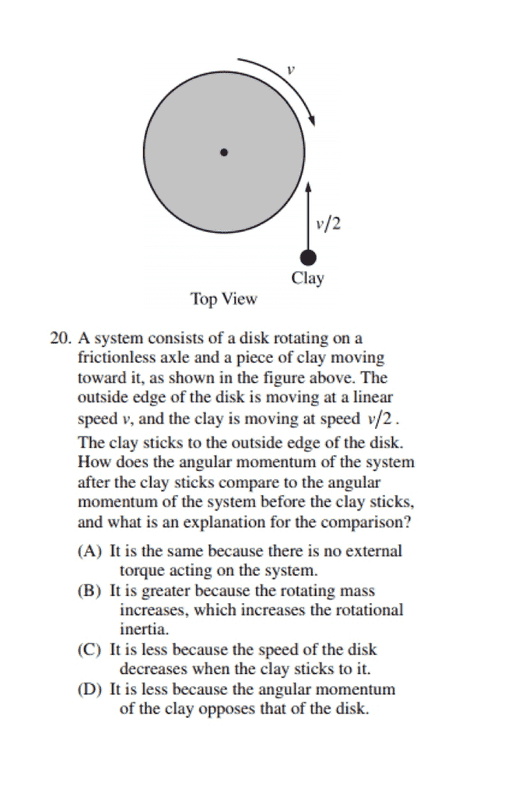
1. A system consists of a disk rotating on a frictionless axle and a piece of clay moving toward it as shown above. Outside edge of the disk is moving at a linear speed of V and the clay is moving at speed v/2. How does angular momentum of system after the clay sticks compare to the angular momentum of system before the clay string?
A) It is the same because there is no external torque acting on the system.
B) It is greater because the rotating mass increases, which increases the rotational inertia.
C) It is less because the speed of the disk decreases when the clay sticks to it.
D) It is less because the angular momentum of the clay opposes that of the disk.
I'm trying to prove my teacher wrong but I can't necessarily figure out how to invalidate his argument. He is trying to argue that the clay creates a torque against the wheel, thus making A not the correct answer. However, my own knowledge and every example of this on the internet chose A as the correct answer (my teacher believes the answer to be C).
2. So I guess my question is... Why doesn't the torque of the clay cause a decrease in momentum?3. I believe it is because the wheel exerts an equal and opposite amount of torque on the clay, thanks to Newton's Third Law, but I am not sure if this is correct. As stated before, I believe the answer is A, but my teacher argued that the answer is C.
A) It is the same because there is no external torque acting on the system.
B) It is greater because the rotating mass increases, which increases the rotational inertia.
C) It is less because the speed of the disk decreases when the clay sticks to it.
D) It is less because the angular momentum of the clay opposes that of the disk.
I'm trying to prove my teacher wrong but I can't necessarily figure out how to invalidate his argument. He is trying to argue that the clay creates a torque against the wheel, thus making A not the correct answer. However, my own knowledge and every example of this on the internet chose A as the correct answer (my teacher believes the answer to be C).
2. So I guess my question is... Why doesn't the torque of the clay cause a decrease in momentum?3. I believe it is because the wheel exerts an equal and opposite amount of torque on the clay, thanks to Newton's Third Law, but I am not sure if this is correct. As stated before, I believe the answer is A, but my teacher argued that the answer is C.
