B Why do photons allow Doppler shift

[Buckethead]

If we (a detector) are moving toward a star that emits a single photon (due to its distance) and that photon hits our detector, it will be blue shifted. My question is why. If the color of a photon is a reflection of its energy level and since the speed of the photon is always coming at us at c irrespective of the speed at which we are traveling toward the star, then why does the color of the photon change if we increase our speed?

 

[Paul Colby]

In current theory light is composed of electromagnetic waves that have quantized amplitudes. The wave (of which the photon is the energy (and momentum) absorbed by the detector thus changing the waves state by one amplitude step) is Doppler shifted just like a classical wave would be.

 

[Buckethead]

But why, even if we view the photon as a wave, would it be Doppler shifted if its velocity relative to the detector does not change? It seems to me this is equivalent to being in a plane and talking to someone while the plane is in the air. The velocity of the sound wave does not change relative to you (just like light in my example) and as a result its pitch does not change.

 

[Nugatory]

But why, even if we view the photon as a wave, would it be Doppler shifted if its velocity relative to the detector does not change? It seems to me this is equivalent to being in a plane and talking to someone while the plane is in the air. The velocity of the sound wave does not change relative to you (just like light in my example) and as a result its pitch does not change.

If you consider the receiver to be at rest, then the source is moving towards the receiver. This does not affect the speed with which the waves approach the receiver, but every successive wave crest has to cover slightly distance than the one immediately before it. Thus, the time between the reception of two consecutive crests is not the time between their emission; it is somewhat less because the second crest travels a shorter distance so arrives just a bit sooner than it otherwise would. This will probably be clearer if you try drawing a spacetime diagram showing the paths of successive wave crests through spacetime.

That explains the classical Doppler effect. There is an additional relativistic correction from time dilation because the emitter is moving relative to the receiver.

 

[Herman Trivilino]

If we (a detector) are moving toward a star that emits a single photon (due to its distance) and that photon hits our detector, it will be blue shifted. My question is why. If the color of a photon is a reflection of its energy level and since the speed of the photon is always coming at us at c irrespective of the speed at which we are traveling toward the star, then why does the color of the photon change if we increase our speed?

The speed is the same but the energy is different. It's the energy, not the speed, that determines the frequency (color).

For massive particles the increase in speed with respect to energy approaches zero as the speed approaches $c$. In other words, as you approach speed $c$ huge increases in energy produce negligible increases in speed. My point is that the relationship between speed and energy is strange compared to the non-relativistic relationship and the photon is a purely relativistic particle.

 

[Buckethead]

If you consider the receiver to be at rest, then the source is moving towards the receiver.

I'm specifying a single photon which left the star mellenia ago, when the sensor was at rest and then later accelerated to some modest speed toward the star, so the relative speed between the star and the observer couldn't be a factor

The speed is the same but the energy is different. It's the energy, not the speed, that determines the frequency (color).

But why is the energy different? If the speed of the photon never changes relative to the observer, then why would its energy change?

 

[Nugatory]

I'm specifying a single photon which left the star mellenia ago, when the sensor was at rest and then later accelerated to some modest speed toward the star, so the relative speed between the star and the observer couldn't be a factor

There's no quantum mechanics involved in this problem (aside from statistical effects at the receiver, which are a distraction here) so no photons involved - you have a flash of light traveling from the emitter to the receiver. This flash of light is an electromagnetic wave.

If the receiver is approaching the source, then the crests of the wave will be closer to one another using the frame in which the receiver is at rest than using the frame in which the emitter is at rest. This will become clear if you draw a diagram.

But why is the energy different? If the speed of the photon never changes relative to the observer, then why would its energy change?

The light is moving at $c$ in all frames, but the wavelength is shorter in the frame in which the receiver is at rest. Therefore the frequency and the energy are greater. This is just another example of the general fact that kinetic energy is always frame-dependent; the only surprising thing is that the energy carried by a flash of light is dependent on the frequency and wavelength, not the speed.

 

[Buckethead]

There's no quantum mechanics involved in this problem (aside from statistical effects at the receiver, which are a distraction here) so no photons involved - you have a flash of light traveling from the emitter to the receiver. This flash of light is an electromagnetic wave.

I'm good with this since the property of light (wave or particle) depends on the experiment you are performing, so wave it is.

If the receiver is approaching the source, then the crests of the wave will be closer to one another using the frame in which the receiver is at rest than using the frame in which the emitter is at rest. This will become clear if you draw a diagram.

I'm not sure how to draw a diagram to reflect this, and I get what you are saying with regard to viewing this as the receiver at rest, but let's look at this another way. Suppose the emitter and receiver are at rest and the star emits a short pulse. Sometime later before the light reaches the receiver, the emitter accelerates toward the receiver then coasts to a constant speed. I expect the receiver will detect no color change. Now reverse the experiment and instead accelerate the receiver then coast to a constant speed just before the pulse reaches the receiver. I expect the receiver will see a blue shift. First, is this correct? If so I find this curious since when the pulse was emitted, the relative speed between the two was 0. And at the time the receiver finished accelerating and was in coast mode, its speed relative to the emitter is no longer relevant since the pulse is in space between the two. In other words, the emitter could explode and vanish so that all that's left is the receiver and the pulse of light somewhere in space. The receiver is moving at c relative to the pulse of light and yet when it arrives it will be blue.

The only difference between the emitter accelerating and the receiver accelerating is the acceleration itself. But if the accelerations occur only during the time the pulse is between the emitter and receiver, and if both are moving at a constant velocity relative to each other when the pulse is still in between, then in both cases the situation between the pulse and the receiver is identical. The relative speed between the pulse and receiver remains at c in both cases and in both cases the speed of the emitter should be irrelevant since what the emitter is doing in both cases is isolated from the pulse already on its way.

 

[PAllen]

Another way to look at this is purely kinematically. 4 momentum is a vector that transforms per the Lorentz transform. If something has a 4 momentum in an emission frame, it will have the Lorentz transform of that 4 momentum in another frame, e.g. the receiver. If you Lorentz transform (E,p), then specialize to that case of E=p for a massless particle (or light), you get the relativistic Doppler formula. So given that light must have energy and momentum, it must undergo relativistic Doppler between frames due to Lorentz invariance. I should say, you get the Doppler formula applied to E. Then the energy of a photon determines its frequency.

 

[Nugatory]

Suppose the emitter and receiver are at rest and the star emits a short pulse. Sometime later before the light reaches the receiver, the emitter accelerates toward the receiver then coasts to a constant speed. I expect the receiver will detect no color change. Now reverse the experiment and instead accelerate the receiver then coast to a constant speed just before the pulse reaches the receiver. I expect the receiver will see a blue shift. First, is this correct?

Yes.

If so I find this curious since when the pulse was emitted, the relative speed between the two was 0. And at the time the receiver finished accelerating and was in coast mode, its speed relative to the emitter is no longer relevant since the pulse is in space between the two. In other words, the emitter could explode and vanish so that all that's left is the receiver and the pulse of light somewhere in space. The receiver is moving at c relative to the pulse of light and yet when it arrives it will be blue.

If the light is moving to the right in some given frame, and the frequency of the light is $\nu$ as measured by an observer at rest in that frame:
- If the receiver is moving to the left in that frame at the moment of reception then the frequency in the frame in which the receiver is at rest will be $\nu+a$; the receiver will measure a blueshift.
- If the receiver is moving to the right in that frame at the moment of reception then the frequency in the frame in which the receiver is at rest will be $\nu-b$; the receiver will measure a redshift.
What happens to the emitter after the light is emitted is irrelevant; all that matter is that the frequency was $\nu$ in the frame in which the emitter was at rest at the moment of emission. Likewise, what happens to the receiver before the light is received is irrelevant; all that matters is the speed of the receiver at the moment of reception.

The only difference between the emitter accelerating and the receiver accelerating is the acceleration itself.

We get different results in the emitter-accelerates and the receiver-accelerates cases because after the acceleration:
- in the first one the receiver is at rest in the frame in which the frequency is $\nu$.
- in the second one the receiver is moving to the left in the frame in which the frequency is $\nu$.

 

[robphy]

Along the lines of @PAllen 's comment, here are some energy-momentum diagrams of photons in different frames of reference.
(These were taken from my post to a different question on another site https://physics.stackexchange.com/questions/362125/momentum-conservation-with-photons/363478#363478 )

In the rest frame of the source, light signals of the same frequency are emitted in the forward and backward direction.
(The original question I responded to asked about the velocity of the source after emission.)
The diagram visualizes the conserveration of 4-momentum problem:
$$
\tilde P_{fin}+\tilde {k_1}+\tilde {k_2}=\tilde P_{init}
$$
in the rest frame of the source,
and in the lab frame [which observes the source moving].

Note, in the lab frame,
the forward light-signal's 4-momentum is increased
(compared to that signal's 4 momentum in the rest frame)
and the backward light-signal's 4-momentum decreased (similarly).
Thus, in the lab frame, the light-signals have different frequencies.

 

[phyzguy]

Now reverse the experiment and instead accelerate the receiver then coast to a constant speed just before the pulse reaches the receiver. I expect the receiver will see a blue shift. First, is this correct? If so I find this curious ...

Yes, this is correct. I'm surprised you find this curious. Suppose I throw a baseball at you at 50 miles per hour. While the baseball is in flight, you accelerate towards it to 200 miles per hour. Is it surprising that the baseball will hit harder than if you stayed stationary? I think not. The analogy is not perfect, since light moves at a constant speed, but it shows that the receiver's speed can matter. As Nugatory has explained, the receiver's speed at the point of absorbing the pulse is what matters, because it causes the wave crests to arrive closer together.

 

[PAllen]

I'm good with this since the property of light (wave or particle) depends on the experiment you are performing, so wave it is.

I'm not sure how to draw a diagram to reflect this, and I get what you are saying with regard to viewing this as the receiver at rest, but let's look at this another way. Suppose the emitter and receiver are at rest and the star emits a short pulse. Sometime later before the light reaches the receiver, the emitter accelerates toward the receiver then coasts to a constant speed. I expect the receiver will detect no color change. Now reverse the experiment and instead accelerate the receiver then coast to a constant speed just before the pulse reaches the receiver. I expect the receiver will see a blue shift. First, is this correct? If so I find this curious since when the pulse was emitted, the relative speed between the two was 0. And at the time the receiver finished accelerating and was in coast mode, its speed relative to the emitter is no longer relevant since the pulse is in space between the two. In other words, the emitter could explode and vanish so that all that's left is the receiver and the pulse of light somewhere in space. The receiver is moving at c relative to the pulse of light and yet when it arrives it will be blue.

The only difference between the emitter accelerating and the receiver accelerating is the acceleration itself. But if the accelerations occur only during the time the pulse is between the emitter and receiver, and if both are moving at a constant velocity relative to each other when the pulse is still in between, then in both cases the situation between the pulse and the receiver is identical. The relative speed between the pulse and receiver remains at c in both cases and in both cases the speed of the emitter should be irrelevant since what the emitter is doing in both cases is isolated from the pulse already on its way.

The situation is not symmetric at all. What the emitter does after emission is obviously wholly irrelevant, as is what the receiver does after reception. If the emetter changes speed before emission, that will have an effect. If the receiver changes speed before reception, that will have an effect. Both of these before/after statements are invariant because they events along one world line (timelike).

 

[jartsa]

But why, even if we view the photon as a wave, would it be Doppler shifted if its velocity relative to the detector does not change? It seems to me this is equivalent to being in a plane and talking to someone while the plane is in the air. The velocity of the sound wave does not change relative to you (just like light in my example) and as a result its pitch does not change.

When you do a small acceleration, everything in the universe changes shape (for you). The change is very small for slow moving objects, not very small for fast moving objects. Lorentz-contraction formula can be used to calculate the change of shapes of all things, except those 'things' that move at the speed of light. If we use 0.99999c as the speed that the light pulse moves, we get almost correct results using the Lorentz-contraction formula.

And the derivation of a general contraction formula is trivial.Oh yes this was about energy. During your acceleration there is a (gravitational) potential difference between every point of the universe (for you), and when you do a small acceleration, everything in the universe changes energy (for you). The amount of change is the original energy of the object multiplied by the potential between the starting position and end position of the object.

Typically fast moving objects, like light pulses, have a large distance between their starting position and end position.

 

[Herman Trivilino]

But why is the energy different? If the speed of the photon never changes relative to the observer, then why would its energy change?

Ask yourself why you expect that the energy should depend on the speed? In non-relativistic physics we expect the energy to be proportional to the square of the speed, but that is just the non-relativistic approximation. It's flawed and the flaws become more and more apparent the closer you get to speed $c$. At speed $c$ there is no dependence at all. Photons of various energies all have the same speed.

 

[Wes Tausend]

Skinnier, but taller photons. :)

 

[Buckethead]

Thanks everyone for contributing to the answers. I've read everyone's post carefully, (understanding some more than others) and enjoy that it is indeed clearing my head a little. I understand the conclusions and have no reservations that red/blue shift occur under the stated circumstances, but am still struggling with this from a strictly logical point of view. Here is my most concise way of putting it:

Emitter and receiver have zero relative velocity. Emitter strikes out, then both emitter and receiver accelerate in the same direction and cease acceleration some time later, all while the pulse of light is somewhere in between the two. At all times the emitter and receiver have zero relative velocity. The pulse reaches the receiver and is blue shifted. During the entire time, the pulse should also have had a velocity of c relative to both the emitter and receiver. Therefore, since the only players in question are the emitter, the pulse, and the receiver and since their relative velocities never changed there should not have been a blue shift.

Do I see a flaw in my argument? Yes. From a third frame watching this whole thing from the side the acceleration caused the relative velocities between the pulse and the receiver to change hence we have blue shift. So there is a way out, but I still don't understand why, if the velocity between the receiver and the pulse never changed from the perspective of the receiver, why it would see blue shift. Not sure I'll ever really understand this.

 

[Ibix]

At all times the emitter and receiver have zero relative velocity.

Not true in relativity from the receiver's perspective due to the relativity of simultaneity - see Bell's spaceship paradox.

 

[PAllen]

I am not sure what the confusion is, but I'll try another clarification. The only thing that matters for Doppler in SR is the relative velocity between the emitter at the emission event and the receiver at the corresponding reception event. What the emitter or receiver do before or after these events is wholly irrelevant (for that reception event). Simultaneity is irrelevant.The Doppler then results from the Lorentz boost for this relative velocity. The analysis can be done in any frame because the relative velocity described is frame invariant.

 

[jartsa]

If we use 0.99999c as the speed that the light pulse moves, we get almost correct results using the Lorentz-contraction formula.

I mean we pick some speed close to c as the the speed that the light pulse moves according to the observer before the observer has accelerated. When the observer accelerates some small amount the speed that the light pulse moves according to the observer changes a tiny amount.

 

[jartsa]

I am not sure what the confusion is, but I'll try another clarification. The only thing that matters for Doppler in SR is the relative velocity between the emitter at the emission event and the receiver at the corresponding reception event. What the emitter or receiver do before or after these events is wholly irrelevant (for that reception event). Simultaneity is irrelevant.The Doppler then results from the Lorentz boost for this relative velocity. The analysis can be done in any frame because the relative velocity described is frame invariant.

Why does the light source seem to become time dilated according to an observer that accelerates relative to the light source?

If light was emitted by a non-time dilated star, how does the light become indistinguishable from a light emitted by a time dilated star, just by acceleration of the observer?

I think the only thing that matters for Doppler in SR is the relative velocity between the emitter and the observer at the observation event. And observer decides what the relative velocity is, light source's opinion is not needed.

Oh yes, a wise observer would say: "I do not know the current velocity of the distant star". So it is the observer's current opinion about the star's past velocity that determines the redshift that the observer observes currently.

 

[Nugatory]

I think the only thing that matters for Doppler in SR is the relative velocity between the emitter and the observer at the observation event.

As with the classical Doppler effect, the relative velocity of the emitter and the observer at the time of observation is irrelevant. (And note that because the emitter and receiver are not colocated, the phrase "relative velocity between the emitter and the observer at the observation event" makes no sense - they aren't both be at the observation event).

You can pick any frame at all, and in that frame the wave will have a particular frequency. In other frames, it will have a different frequency.

Thus, if the wave has a given frequency in some frame, and the receiver is in motion in that frame, then in the frame in which the receiver is at rest at the moment of the reception event there will a Doppler shift in one direction or the other.

The only reason that the speed of the emitter ever comes into the picture is that it is particularly convenient to calculate the frequency of the wave in the frame in which the emitter is at rest at the moment of emission. Once we've established what that frame is, it is irrelevant whether the emitter remains at rest in that frame or not; we know what the frequency of the wave is in that frame. And from there we can ask the next question: is the receiver at rest in that frame at the moment of reception? If not, there's non-zero Doppler.

 

[Herman Trivilino]

Emitter and receiver have zero relative velocity. Emitter strikes out, then both emitter and receiver accelerate in the same direction and cease acceleration some time later, all while the pulse of light is somewhere in between the two. At all times the emitter and receiver have zero relative velocity. The pulse reaches the receiver and is blue shifted. During the entire time, the pulse should also have had a velocity of c relative to both the emitter and receiver. Therefore, since the only players in question are the emitter, the pulse, and the receiver and since their relative velocities never changed there should not have been a blue shift.

I'll try to re-write the scenario, eliminating the acceleration portion of the thought experiment.

Emitter and receiver have zero relative velocity, and are at rest relative to an Observer A, but are in motion along a line joining them according to Observer B. The pulse reaches the receiver and is blue shifted is B's frame^*. During the entire time, the pulse should also have had a velocity of c relative to both the emitter and receiver. Therefore, since the only players in question are the emitter, the pulse, and the receiver and since their relative velocities never changed there should not have been a blue shift in A's frame.

^*Edit: Note that the receiver will not show this blue shift, and B will reckon it's because the receiver is in motion relative to him.

 

[PAllen]

Why does the light source seem to become time dilated according to an observer that accelerates relative to the light source?

Read what wrote carefully. The acceleration of the receiver, per se, is irrelevant. A consequence of the acceleration is that the receiver has a relative velocity at reception event compared to emitter at emission event. This is the sole source of redshift/blueshift between the front and back of an accelerating rocket.

If light was emitted by a non-time dilated star, how does the light become indistinguishable from a light emitted by a time dilated star, just by acceleration of the observer?

This is not meaningful. What is a time dilated star?? There is no such category in SR.

I think the only thing that matters for Doppler in SR is the relative velocity between the emitter and the observer at the observation event. And observer decides what the relative velocity is, light source's opinion is not needed.

Completely wrong. The motion of the emitter 'at reception time' is irrelevant and ambiguous - whose simultaneity? Doppler is an invariant phenomenon that does not involve simultaneity at all. There are two events (one emission event on the world line of the emitter, one reception event on the world line of the receiver). These world lines have velocities at these events. The two velocity values are frame dependent. The relative velocity is frame independent in SR.

Oh yes, a wise observer would say: "I do not know the current velocity of the distant star". So it is the observer's current opinion about the star's past velocity that determines the redshift that the observer observes currently.

This thread is wholly about SR, not GR, so let's not muddy it with cosmology GR consideration. Relative velocity is unambiguous in SR.

 

[PAllen]

As with the classical Doppler effect, the relative velocity of the emitter and the observer at the time of observation is irrelevant. (And note that because the emitter and receiver are not colocated, the phrase "relative velocity between the emitter and the observer at the observation event" makes no sense - they aren't both be at the observation event).

In SR, relative velocity at a distance is unambiguous. I agree completely with everything else you wrote.

 

[Dale]

I still don't understand why, if the velocity between the receiver and the pulse never changed from the perspective of the receiver, why it would see blue shift.

I think you have to just let go of this concept. The quantity you are focusing on is the instantaneous relative velocity of two spatially separated objects. This quantity never has any physical significance in any scenario whatsoever. Thinking that it does will lead to confusion such as this. The measured Doppler shift cannot depend on it, because no physical quantity can. It is a frame-dependent quantity, and no reference frame is privileged.

Does that make sense? You must empty your mind of this incorrect idea before you can fill it with the correct idea.

 

[Nugatory]

In SR, relative velocity at a distance is unambiguous. I agree completely with everything else you wrote.

Ah - yes, of course you're right.

 

[sweet springs]

since the speed of the photon is always coming at us at c irrespective of the speed at which we are traveling toward the star, then why does the color of the photon change if we increase our speed?

Say a particle of non zero mass m has four velocity $(u_0,u_1,u_2,u_3)$ of norm 1. Multiplied by m $m(u_0,u_1,u_2,u_3)$ is four-momentum $(p_0,p_1,p_2,p_3)$ of norm m. Momentum is given by velocity.
Photon with zero mass does not have four velocity but four-momentum $(p_0,p_1,p_2,p_3)$ of norm zero. You cannot expect proportional relation of four-velocity and four-momentum for zero mass particle as you do for non zero mass particle. Momentum varies even if speed is the same c.

Wave picture is shared among zero and non zero particles. Four wave number $(k_0,k_1,k_2,k_3)$ = $\frac{1}{\hbar}(p_0,p_1,p_2,p_3)$ for both de-Broglie wave and light wave.

 

[robphy]

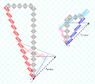
Hopefully this diagram will help clarify what many of us have been trying to say.

These diagrams are doing double duty as a spacetime diagram and as energy-momentum diagrams.
We draw these diagrams on rotated graph paper
to help visualize the light-signals and to visualize the unit tickmarks on observer worldlines.

The key idea is that:
once the light-signal with 4-momentum p_emitted is emitted by the instantaneous emitter at E,
it travels along to event R on E's future light-cone along the direction of p_emitted.
The emitter had influence on this 4-momentum only at E---what the emitted did before or after E doesn't matter.
The 4-momentum of the light-signal arrives at event R (call it p_received)
and can be measured by a instantaneous receiver at event R.
What the receiver did before R or does after R doesn't affect that measurement at R.

[Of course, since R and E are lightlike related,
there is no frame of reference where R and E are simultaneous... and
there is no frame of reference that can visit both R and E.]

For completeness...

In the emission diagram,
the source is moving with velocity v_{emitter,lab}=-5/13 and emits a forward light-signal [with velocity +c] with energy=6.
The lab frame measures that energy to be 4 units (thus redshifted).
Indeed k_{emitter,lab}=\sqrt{\frac{1+v_{emitter,lab}}{1-v_{emitter,lab}}}=\sqrt{\frac{1+(-5/13)}{1-(-5/13)}}=\frac{2}{3}.

In the reception diagram,
the lab frame would still measure that energy to be 4 units (no Doppler shift).
Since the receiver is moving with velocity v_{receiver,lab}=3/5, the receiver would measure energy=2.
Indeed k_{receiver,lab}=\sqrt{\frac{1+v_{receiver,lab}}{1-v_{receiver,lab}}}=\sqrt{\frac{1+(3/5)}{1-(3/5)}}=2.

From the emitter frame,
v_{receiver,emitter}=4/5 (check: v_{re,em}=\frac{v_{re,lab}-v_{em,lab}}{1-v_{re,lab}v_{em,lab}}=\frac{(3/5)-(-5/13)}{1-(3/5)(-5/13)}=4/5)
so, the relative-doppler factor is
k_{re,em}=\sqrt{\frac{1+v_{re,em}}{1-v_{re,em}}}=\sqrt{\frac{1+(4/5)}{1-(4/5)}}=3. (check: k_{re,em}=\frac{k_{re,lab}}{k_{em,lab}}=\frac{(2)}{(2/3)}=3).

From the receiver frame,
v_{em,re}=(-v_{re,em})=-4/5
and k_{em,re}=(1/k_{re,em})=1/3.
This explains the received redshifted light-signal of energy 2, compared to the emitted energy 6.

 

[Buckethead]

I am not sure what the confusion is, but I'll try another clarification. The only thing that matters for Doppler in SR is the relative velocity between the emitter at the emission event and the receiver at the corresponding reception event. What the emitter or receiver do before or after these events is wholly irrelevant (for that reception event). Simultaneity is irrelevant.The Doppler then results from the Lorentz boost for this relative velocity. The analysis can be done in any frame because the relative velocity described is frame invariant.

This is a very concise description of what happens and sums things up nicely regarding the question of "what happens". My frustration is the "why". This morning I came up with a better example of my concern:

An inertial emitter sends out a pulse of red light. The pulse itself, traveling away at c has no doppler shift information as that is undefined until a reception is made. This is in contrast to a sound wave for example where the relative velocity between the emitter and the air determines the frequency of the sound wave. Again I want to clarify that the pulse has no information in it that would indicate the velocity of the source. Many years later a ship arrives out of warp from the Delta Quadrant and smacks right into the pulse. The pulse hits the ship at the expected speed of c from the frame of the ship. The ships sensors measure the frequency of the pulse and find it is blue in color. Considering that there is no way for the light pulse to have encoded any speed information from the emitter (since it will always be emitted at c) why is the pulse now blue when it was emitted with a red color.

 

[Buckethead]

I see a great many new posts just came in since PAllens post was posted that I did not see when I wrote my most recent response, so I need to go through all of them. So unless my recent post raises a new concern, no need to respond until I can get through all these new posts with hopefully a new sense of enlightenment.

 

[Nugatory]

The pulse itself, traveling away at c has no doppler shift information as that is undefined until a reception is made.

It does, however, have a frame-dependent frequency; and it has this frame-dependent property whether it eventually encounters a receiver or not.

You are thinking of the frequency in the frame in which the emitter was at rest at the moment of emission as the "real" or unshifted frequency. It's not; that frame is no more special than any other frame.

 

[Herman Trivilino]

Considering that there is no way for the light pulse to have encoded any speed information from the emitter (since it will always be emitted at c) why is the pulse now blue when it was emitted with a red color.

When you say it was emitted with a red color what do you mean? That in the rest frame of the emitter it was red?

 

[Buckethead]

When you say it was emitted with a red color what do you mean? That in the rest frame of the emitter it was red?

Yes.

 

[Buckethead]

You can pick any frame at all, and in that frame the wave will have a particular frequency. In other frames, it will have a different frequency.

Key point.

It does, however, have a frame-dependent frequency; and it has this frame-dependent property whether it eventually encounters a receiver or not.

Now we're getting to the meat and potatoes and I appreciate that you said this. I need to offer up an amusing way to look at this. (PLEASE read this for amusement only*)

It occurs to me that frame dependent frequency and frame dependent property might be two different things and I offer up my definition that frame dependent frequency refers to two frames, the emitter during emission and the receiver during reception. Combined, these result in a specific frequency upon reception. I further offer the definition that frame dependent property as used here should be called an emitter frame dependent property and is a property with a value set by the emitter during emission only. A frame dependent frequency cannot be a property of the light pulse because the receiving frame is still undefined while the pulse is in transit but a emitter frame dependent property can be.

it makes sense that the light pulse would contain an (emitter) frame dependent property that would be a constant which is set at the time of emission. It is now possible for the pulse to roam freely with no strings attached to the emitter as long as it holds this constant. The receiver also has an inherent frame dependent property, the value of which is not determined by the emitter or the pulse.

The final frequency of the light pulse is a function of both the emitter frame dependent property value encoded in the pulse and the frame dependent property value of the receiver.

The emitter frame dependent property can be encoded into the light pulse's frequency and would be different than the frequency of the emitter because it would contain information both about the frequency of the emitter hardware and of the emitter frame dependent property value.

The only problem with this idea is that I don't know what might determine the emitter frame property value during emission or the receiver property value during reception. Again, my apologies for going out on a limb here. I know that is frowned upon but I couldn't help myself. This is just a really fun thought.

*To everyone reading please do not construe this as a speculation as to what I think might be happening behind the scenes, but instead please read it only as an interesting analogy to what actually is happening, such as a change in momentum as was offered up earlier or some other mechanism. It just seems to me that what I'm going to mention here is an interesting way to sort through this from a purely logical standpoint in a world where "that's just the way it is" is used too much.

 

[Buckethead]

I think you have to just let go of this concept. The quantity you are focusing on is the instantaneous relative velocity of two spatially separated objects. This quantity never has any physical significance in any scenario whatsoever. Thinking that it does will lead to confusion such as this. The measured Doppler shift cannot depend on it, because no physical quantity can. It is a frame-dependent quantity, and no reference frame is privileged.

Does that make sense? You must empty your mind of this incorrect idea before you can fill it with the correct idea.

Thank you. That was well put. And I get that this is the case for specially separated objects (the pulse and the receiver). But at the time of measurement, the instantaneous relative velocity can be measured and that value will be c so why is that not what is important?

 

[Buckethead]

Hopefully this diagram will help clarify what many of us have been trying to say.

Thank you for posting that detailed description and graphs. I need to study it a bit to fully grasp it.

 

[Herman Trivilino]

Yes.

So, it wasn't that it was red, it was that it was red in that frame of reference. In another frame of reference it's blue.

 

[Bartolomeo]

Considering that there is no way for the light pulse to have encoded any speed information from the emitter (since it will always be emitted at c) why is the pulse now blue when it was emitted with a red color.

Relativistic Doppler shift is very simple. For example, if a source and an observer move towards each other, proper frequency of the source (for example it was red) the observer will see blueshifted. Cause of this blueshift he can explain doubly:

a) An observer is "at rest" and the source moves towards the observer - the source’s clock dilates, so the source oscillates slower.

$$\omega = \frac {\omega_0 \sqrt {1-v^2/c2}}{1-v/c}$$

If velocity of the source $v$ was close to $c$, according to this formula “classic” frequency would be “very infinitely intense” and all the waves would have gathered in a heap straight in front of the source. But Lorentz – factor (dilation of the source’s clock) “reduces” that frequency to $\omega$.

b) The source is "at rest" and the observer moves toward it, so the observer’s clock (and observer himself) slows down. Proper frequency was “red”, but it turns into “blue” due to dilation of observer’s clock.

$$\omega = \frac {\omega_0 (1+v/c)} {\sqrt {1-v^2/c2}}$$

If velocity of an observer $v$ was close to $c$, according to this formula “classic” frequency would be $2\omega_0$, but Lorentz – factor (dilation of observer’s clock) “increases” it to $\omega$. That means the observer turns into a "dawdler" himself.

Outcome will be the same - measured frequency will be $\omega$, but the reasons are frame - dependent. Feynman considers the both cases in his lectures – Relativistic Doppler Effect

http://www.feynmanlectures.caltech.edu/I_34.html

Worth to note, that Einstein himself described exactly the “moving observer” case in his 1905 article:

https://www.fourmilab.ch/etexts/einstein/specrel/www/ - § 7. Theory of Doppler's Principle and of Aberration

From the equation for $\omega'$ it follows that if an observer is moving with velocity $v$ relatively to an infinitely distant source of light of frequency $\nu$, in such a way that the connecting line “source-observer” makes the angle $\varphi$ with the velocity of the observer referred to a system of co-ordinates which is at rest relatively to the source of light, the frequency $\nu '$ of the light perceived by the observer is given by the equation

$$\nu' = \nu \frac {1-\cos \varphi v/c}{\sqrt {1-v^2/c^2}}$$

We see that, in contrast with the customary view, when $v= -c, \nu' = \infty$

It follows from these results that to an observer approaching a source of light with the velocity $c$, this source of light must appear of infinite intensity.

Again, the formula shows, that in classical case (if $v = -c$) measured by a moving observer frequency would be $2\nu$. Wavefronts and the observer approach each other with equal velocities. According to Einstein, if an observer moves towards a source, we must divide this frequency by $\sqrt {1-v^2/c^2}$, i.e. “actual” frequency $\nu$ appears $\sqrt {1-v^2/c^2}$ times more intense due to dilation of the observer’s clock. That means, the observer sees that processes around him happen not slower, but faster.

Quite strange, that Einstein himself looked at Doppler Shift “by eyes of moving observer”, because this case graphically demonstrates, that the source's clock is running not slower, but $\sqrt {1-v^2/c^2}$ times faster than observer's own clock. In Special Relativity an observer never moves himself, but Einstein has made some exception.

It is exactly as in the Lorentz theory.

Page 59 - http://www.mpiwg-berlin.mpg.de/litserv/diss/janssen_diss/Chapter3.pdf

 

[Dale]

I get that this is the case for specially separated objects (the pulse and the receiver).

The spatially separated objects I was referring to are the emitter and the reciever.

The physically meaningful relative velocity is the relative velocity between the emitter at the time of emission and the receiver at the time of reception.

 

[Nugatory]

It occurs to me that frame dependent frequency and frame dependent property might be two different things

There are many frame-dependent properties. Frequency is one of them. Thus, "frame dependent frequency" and "frame dependent property" are different things in the same way that elephants and animals are different things: An elephant is an animal, but there are animals that are not elephants.

and I offer up my definition that frame dependent frequency refers to two frames, the emitter during emission and the receiver during reception.

That might be the root of your misunderstanding right there. The frequency in any given frame is defined as $\nu=1/\Delta{t}=c/\lambda$ where $\Delta{t}$ is the time between the arrival of successive wave crests and $\lambda$ is the distance between successive wave crests. This quantity is well defined and can be calculated in any frame as long as you know what it is in some frame.

 

[Dale]

@Buckethead the best online reference I know for the Doppler effect is here

http://www.mathpages.com/rr/s2-04/2-04.htm

 

[PAllen]

This is a very concise description of what happens and sums things up nicely regarding the question of "what happens". My frustration is the "why". This morning I came up with a better example of my concern:

An inertial emitter sends out a pulse of red light. The pulse itself, traveling away at c has no doppler shift information as that is undefined until a reception is made. This is in contrast to a sound wave for example where the relative velocity between the emitter and the air determines the frequency of the sound wave. Again I want to clarify that the pulse has no information in it that would indicate the velocity of the source. Many years later a ship arrives out of warp from the Delta Quadrant and smacks right into the pulse. The pulse hits the ship at the expected speed of c from the frame of the ship. The ships sensors measure the frequency of the pulse and find it is blue in color. Considering that there is no way for the light pulse to have encoded any speed information from the emitter (since it will always be emitted at c) why is the pulse now blue when it was emitted with a red color.

I already answered the 'why' accepting that you wanted to consider a particle point of view rather than a wave point of view. Any particle carries an energy and momentum. The combination of these form a Lorentz covariant vector. This means that the energy and momentum are frame dependent, transforming via the Lorentz transform. The norm of this vector is the mass, which is zero in the case of a photon. The behavior of this vector is the same for a photon, a proton, or a baseball. If emitted with some energy and momentum per some emission frame, no matter where or when the particle is measured, its energy or momentum will be given by the Lorentz transform corresponding to the velocity of the detector in the original emission frame, applied to the energy/momentum as specified in the emitter frame.

Thus what any particle encodes (to use your terminology) is an energy and momentum for any possible measurement frame. It is best to think of this as one vector property, with different expression in different frames. The only thing specific to a photon is that its energy is proportional to its frequency = color (and its mass is zero). Note that no information about the motion of the emitter is really encoded. What is encoded is this vector property specifying how the the particle would be measured in any frame. One that happens to be the same as the emission event rest frame, will measure the same energy as the original emitter would.

Maybe it will be clearer to forget the emission frame and just talk about a photon that per some arbitrary frame would have energy E and momentum p. Then because it has no mass, the magnitude of the momentum is E (remember E² - p² = m, which is zero). Then, the momentum 4 vector for the light can be written E(1,k) ,where k is a unit 3 vector in the spatial direction of the light's (photon, if you will) motion. Now imagine an arbitrary detector with 4-velocity γ(1,v), where v is the 3-vector velocity of the detector. Then the energy measured by the detector will be the time component of the momentum vector expressed in the detector's rest frame, which is just given by the vector product of the momentum 4-vector and detector 4-velocity, generally: γE(1-k⋅v) . In the co-linear case, with v and k in the same direction, this simply becomes γE(1-v), which with trivial algebra is E√((1-v)/(1+v)), which is the standard relativistic Doppler factor applied to energy. Then, in the case of a photon, this factor applies to frequency as well.

 

[Buckethead]

I already answered the 'why' accepting that you wanted to consider a particle point of view rather than a wave point of view. Any particle carries an energy and momentum. The combination of these form a Lorentz covariant vector. This means that the energy and momentum are frame dependent, transforming via the Lorentz transform. T

Sorry for the delayed response. I've been trying to digest all this to see where the flaws in my logic are. It occurred to me that the heart of my question does not require relativistic speeds and in fact that confuses the issue. After fooling around on a spread sheet it turns out that if the speed between the emitter and receiver is only 1000MPH, the Newtonian part of the Doppler shift formula is much much larger than the relativistic part. (about 136,000:1) I originally thought that the problem could be solved, as many here have mentioned, if you just consider that energy of the photon or the frequency of the pulse are changed between the transmitter and receiver by the Lorentz factor. However, that is only a very small part of it. Let's look at this at much slower speeds.

A ship (A) is stationed at a place where a pulse of light of duration 1 second (duration as measured by ship A) is coming from the left, and a ship (B) coming from the right at v=1000MPH collide. Ship B measures the speed of the incoming light and of course it is c. It also measures the duration. Ship A however calculates that ship B and the light beam have collided at c+v. It also therefore calculates that the duration of the pulse as seen by ship B must be 1-v/c. According to Doppler theory ship B will also measure the duration to be 1-v/c. The question is, how can this be? For one thing, all measuring instruments on A and B match up to within the Lorentz factor. In other words, there is insignificant length contraction and time dilation. It's easy to see why ship A's measurement is accurate. But ship B cannot measure 1-v/c because the incoming pulse is colliding from B's frame at c, not c+v. It might seem like ship B is measuring a shorter pulse (shorter by 1-v/c), but again, A has measured the pulse and it is exactly 1 second.

 

[PeroK]

@Buckethead it seems to me your problem is trying to think of frequency, energy and momentum of the photon as an absolute property of the photon, independent of reference frame. The energy of a photon is not related to its speed (which is frame independent) but to its frequency (which is frame dependent).

If you're moving towards a light source, you cannot measure the same photon energy as the source. However that energy is produced, it cannot be the same in the two frames. Energy must transform between frames.

Any interaction of a photon with a massive object (including the star that produced it) must have a balanced energy-momentum equation in every frame. The energy of the photon, therefore, must be frame dependent and cannot be an absolute instrinsic property of the photon.

In terms of the mechanism, it seems to me this was perfectly explained by @Nugatory in post #4.

 

[Dale]

Sorry for the delayed response. I've been trying to digest all this to see where the flaws in my logic are. It occurred to me that the heart of my question does not require relativistic speeds and in fact that confuses the issue. After fooling around on a spread sheet it turns out that if the speed between the emitter and receiver is only 1000MPH, the Newtonian part of the Doppler shift formula is much much larger than the relativistic part. (about 136,000:1) I originally thought that the problem could be solved, as many here have mentioned, if you just consider that energy of the photon or the frequency of the pulse are changed between the transmitter and receiver by the Lorentz factor. However, that is only a very small part of it. Let's look at this at much slower speeds.

A ship (A) is stationed at a place where a pulse of light of duration 1 second (duration as measured by ship A) is coming from the left, and a ship (B) coming from the right at v=1000MPH collide. Ship B measures the speed of the incoming light and of course it is c. It also measures the duration. Ship A however calculates that ship B and the light beam have collided at c+v. It also therefore calculates that the duration of the pulse as seen by ship B must be 1-v/c. According to Doppler theory ship B will also measure the duration to be 1-v/c. The question is, how can this be? For one thing, all measuring instruments on A and B match up to within the Lorentz factor. In other words, there is insignificant length contraction and time dilation. It's easy to see why ship A's measurement is accurate. But ship B cannot measure 1-v/c because the incoming pulse is colliding from B's frame at c, not c+v. It might seem like ship B is measuring a shorter pulse (shorter by 1-v/c), but again, A has measured the pulse and it is exactly 1 second.

I have no idea what you are trying to calculate here.

If you are willing to do the calculation, then just do the full fledged Doppler calculation. Say the beginning of one cycle is emitted at t=0 so the beginning of the next cycle is emitted at t=T where T is the period (1/f). Then simply calculate when the beginning of each cycle is received and subtract to get the received period.

You can simplify it even further if you use Bondi’s “k calculus” approach.

 

[Buckethead]

@Buckethead it seems to me your problem is trying to think of frequency, energy and momentum of the photon as an absolute property of the photon, independent of reference frame.

I don't think I am. I understand that in Newtonian kinematics the momentum of an object is determined by (for example) the relative velocity between the object and another object when they collide. And it appears we are applying a similar idea to light.

The energy of a photon is not related to its speed (which is frame independent) but to its frequency (which is frame dependent).

OK good. Since the speed is always c this makes sense that the momentum must then be defined by the lights frequency.

If you're moving towards a light source, you cannot measure the same photon energy as the source. However that energy is produced, it cannot be the same in the two frames. Energy must transform between frames.

Yes, this appears to be the case.

Any interaction of a photon with a massive object (including the star that produced it) must have a balanced energy-momentum equation in every frame. The energy of the photon, therefore, must be frame dependent and cannot be an absolute instrinsic property of the photon.

Yes, again this appears to be the case.

In terms of the mechanism, it seems to me this was perfectly explained by @Nugatory in post #4.

Actually, to me, no, it doesn't. Here is my problem.

If you consider the receiver to be at rest, then the source is moving towards the receiver. This does not affect the speed with which the waves approach the receiver, but every successive wave crest has to cover slightly distance than the one immediately before it.

This is totally a Newtonian kinematic viewpoint. It implies that the wave is traveling in a medium and the ship is moving through that medium at some velocity causing the crests of the waves to be closer together. This works fine for sound, but I don't see how it can for light because c is frame independent. For example imagine someone throws a baseball at you at 50MPH. There is a certain momentum in that ball relative to you. Now imagine you run at 10MPH toward the pitcher and he throws again, however, because the baseball is light he throws the ball at 40MPH. It still hits you at 50MPH and its pulse width (the width of the ball going past you) is the same as before and therefore its frequency is the same and likewise its momentum is the same. Regardless of how fast you run toward the ball, if the ball always hits you at 50MPH, how can its energy change?

The first thought (for me) is that it's a relativistic problem. But if the ship in question is traveling at a slow speed (1000MPH for example), the frequency shift due to Newtonian kinematics (non-relativistic portion of the Doppler shift formula) is far greater than that determined by the Lorentz formula. So something else is going on.

I do understand that the Doppler shift formula does actually work, so I'm not questioning that its use is proper, but the non-relativistic portion of the Doppler shift formula is Newtonian and I don't know how it can be applied to light if c is frame independent. The issue becomes more clear if you take into account that the Doppler shift felt by the receiver is dependent on the relative speed of the emitter when there is no link whatsoever between the emitter and receiver as would be in the case of sound for example (where the medium for the sound wave determines the relative velocity of the emitter and receiver). If there is no medium to relate the speed of the two, which there isn't, then the only way around this is...well actually, I can't see any way around this.

 

[PeterDonis]

This is totally a Newtonian kinematic viewpoint. It implies that the wave is traveling in a medium and the ship is moving through that medium at some velocity causing the crests of the waves to be closer together.

No, it doesn't. There's no need to postulate a medium. All you need is that the source emits wave crests at some fixed frequency by its clock, and that the source moves closer to the receiver by some distance in between emitting any two successive wave crests. They don't even have to be wave crests; they could be bullets, or very quick pulses of sound. The reasoning is the same: the time between two successive thingies being received by the receiver is different than the time between two successive thingies being emitted by the source, because of the relative motion.

I don't know how it can be applied to light if c is frame independent.

The only difference the frame independence of $c$ makes, if we're talking about purely non-transverse motion (i.e., the relative motion of the source and receiver is all along the line between them) is in the quantitative details of how much Doppler shift there is for a given relative speed. (If you add transverse motion to the mix, things get more complicated, because SR predicts a Doppler shift for tranverse motion while Newtonian mechanics does not. But I don't think we need to get into those complications here.)

 

[Herman Trivilino]

I do understand that the Doppler shift formula does actually work, so I'm not questioning that its use is proper, but the non-relativistic portion of the Doppler shift formula is Newtonian and I don't know how it can be applied to light if c is frame independent.

By that you mean there's a portion of the derivation of the Doppler shift formula that's the same as the derivation that makes use of the Newtonian approximation?

Relativistic physics is not something separate from Newtonian physics. Newtonian physics is just an approximation that works well enough under certain conditions, it can't tell you anything that relativistic physics can't also tell you.

 

[Buckethead]

No, it doesn't. There's no need to postulate a medium. All you need is that the source emits wave crests at some fixed frequency by its clock, and that the source moves closer to the receiver by some distance in between emitting any two successive wave crests. They don't even have to be wave crests; they could be bullets, or very quick pulses of sound. The reasoning is the same: the time between two successive thingies being received by the receiver is different than the time between two successive thingies being emitted by the source, because of the relative motion.

True, a medium is not necessary, as I'm OK with baseballs in space. However it's the same thing. You are still talking as if the relative velocity between the receiver and the light pulse changes. Please explain to me how the energy of the light pulse, or bullets, or pulses of sound can change if its velocity relative to you does not change.

The only difference the frame independence of cc makes...is in the quantitative details of how much Doppler shift there is for a given relative speed.

My understanding is that there is the relativistic (Lorentz transform) amount and then there is the Newtonian Doppler shift. For slow speeds we can easily dismiss the relativistic amount. It's also my understanding that the Newtonian Doppler shift for frame independent and frame dependent things are the same. So what is the quantitative difference that you are referring to?