FallenApple
- 564
- 61
So the picture is this.
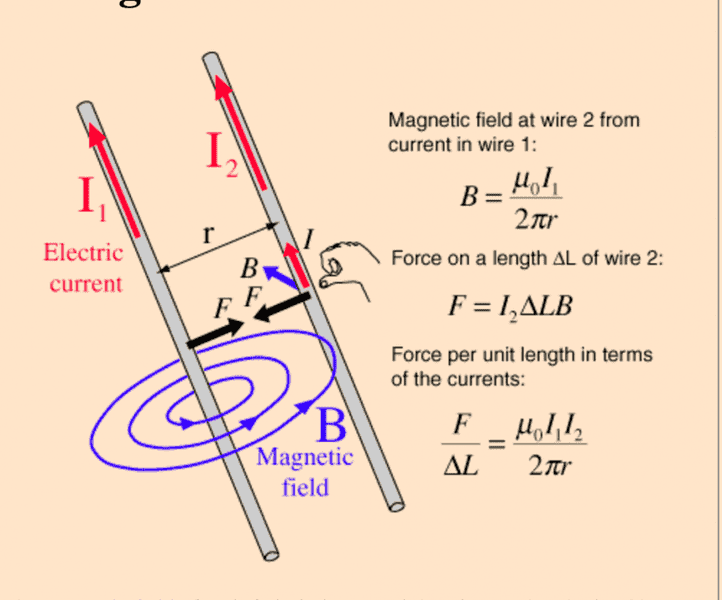
Basically an application of amperes law and Newtons third law shows that they attract.But what about from the frame of reference of the moving currents. Say I have a stream of charges moving to the right, and another stream of charges moving to the right. Both with same velocity and charge density.
Well, in the frame of reference of the moving charges, I just have one row of charges and another row of charges below it. They exert electric forces on each other but not the magnetic force since in this frame, none of the charges are moving relative to each other. If I look at one charge, the left and right charges' effects from the same line cancel. And the left and right charges' effects from the line below will add positively in the vertical while only canceling in the left right direction. And of course, the charge directly below will exert a net force up. In the end, the two currents should be repelling each other when viewed from the frame of reference of the currents.
What resolves this?
Basically an application of amperes law and Newtons third law shows that they attract.But what about from the frame of reference of the moving currents. Say I have a stream of charges moving to the right, and another stream of charges moving to the right. Both with same velocity and charge density.
Well, in the frame of reference of the moving charges, I just have one row of charges and another row of charges below it. They exert electric forces on each other but not the magnetic force since in this frame, none of the charges are moving relative to each other. If I look at one charge, the left and right charges' effects from the same line cancel. And the left and right charges' effects from the line below will add positively in the vertical while only canceling in the left right direction. And of course, the charge directly below will exert a net force up. In the end, the two currents should be repelling each other when viewed from the frame of reference of the currents.
What resolves this?